Question

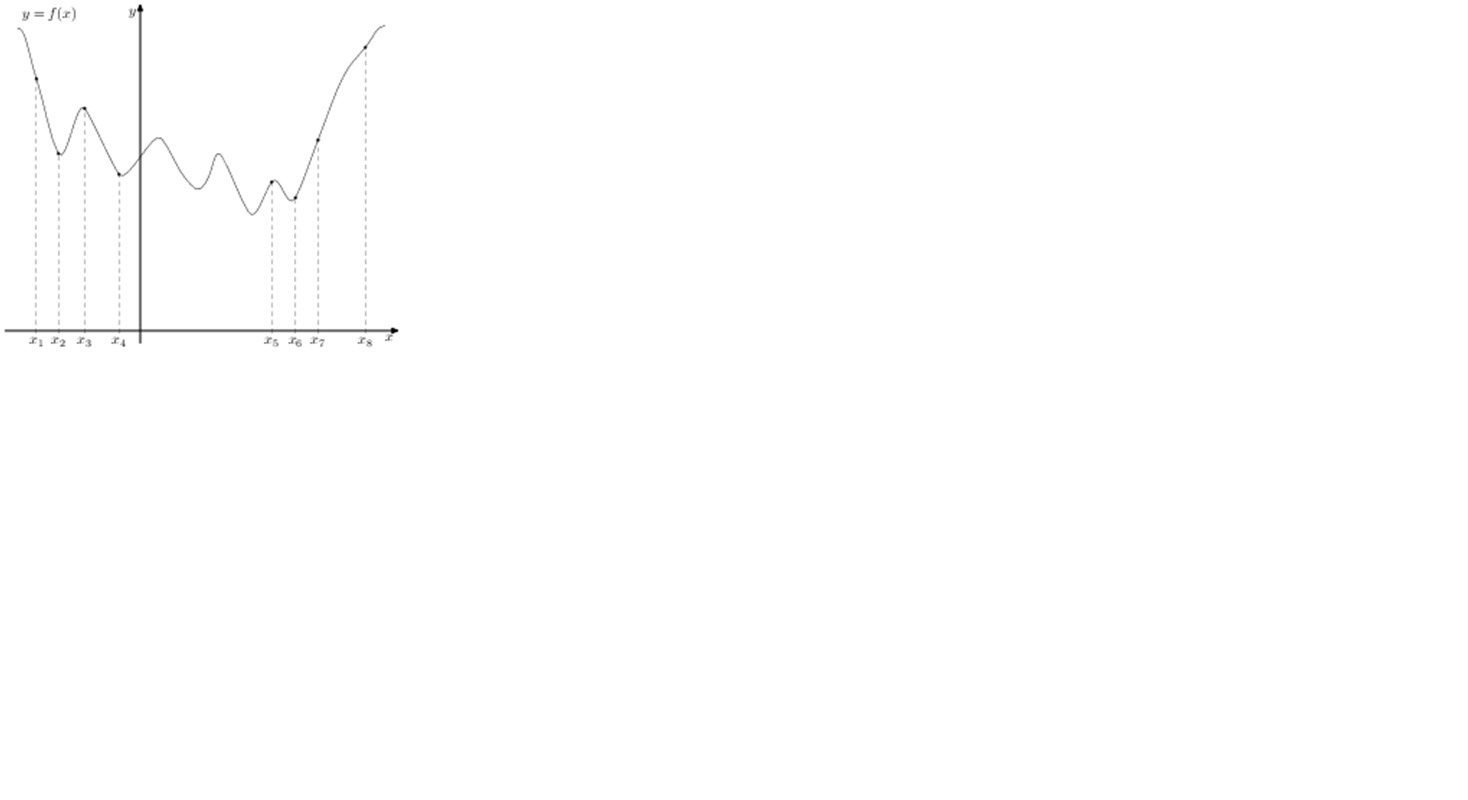
На рисунке изображен график функции y= f(x) и шесть точек на оси абсцисс: x1 x2 x3 x4 x5 x6 x7 x8. В скольких из этих точек производная функции f(x) отрицательна?

Answer 1

В 4, от икс 1 до икс 4, производная отрицательная, так как касательные к этим точкам - прямые y = kx + b, где k < 0, это можно видеть по тому, что эти прямые проходят через 2 и 4 координатные четверти

Answer 2

можно точнее

Answer 3

По сути производная - изменение функции к изменению аргумента на промежутке, длина которого стремитсч к нулю (почитайте про пределы). Таким образом, о производной можно судить по касательной к нужной точке. Если касательная идет из нижнего левого угла в верхний правый (1 и 3 коорд четверти), то производная положительна, так как линия касательной монотонно возрастает. И наоборот, если 2 и 4 четверти, то производная отрицательна. Проведите касательные к точкам на графике и увидите