Question

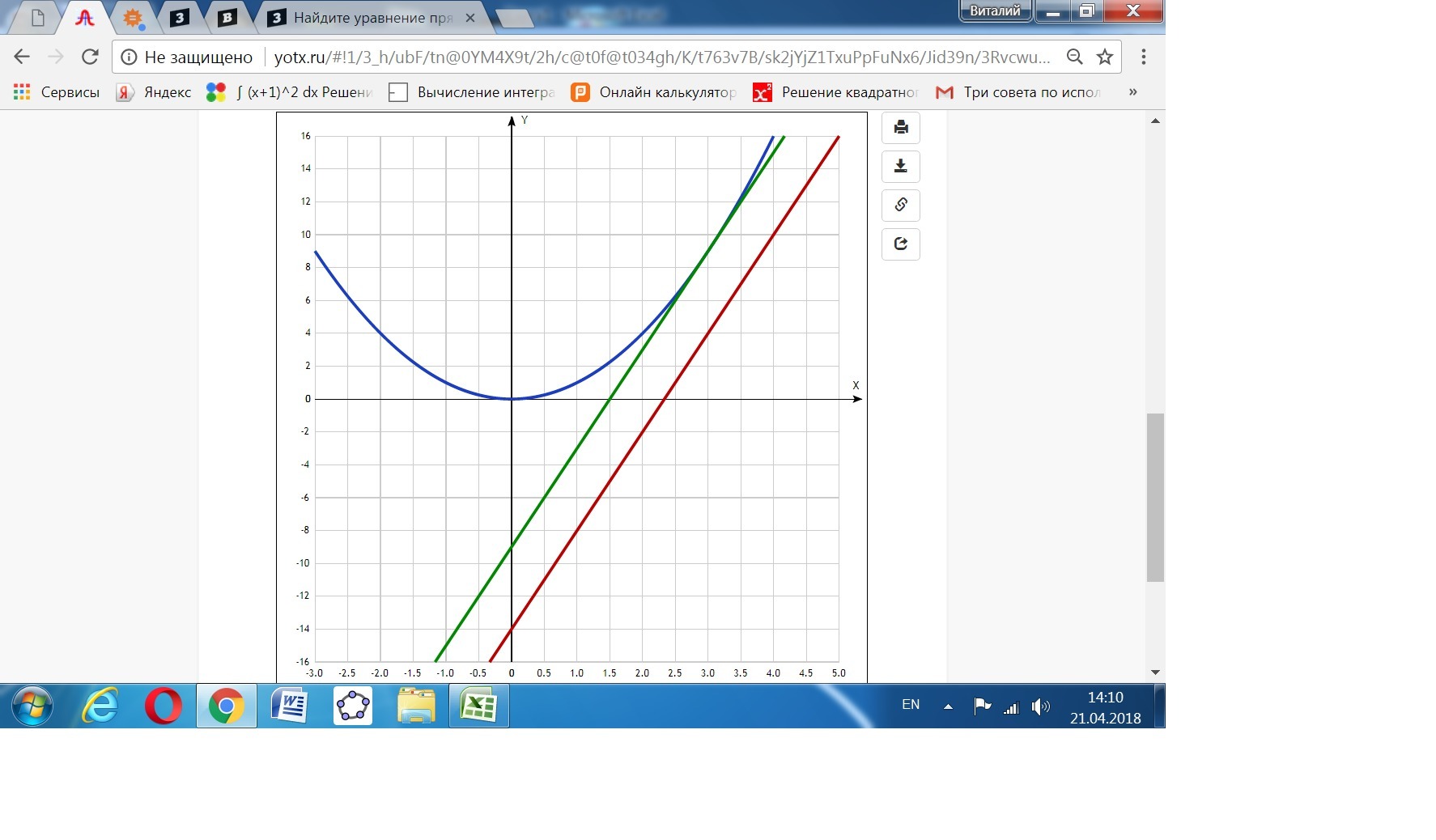
Найдите уравнение прямой, проходящей через точку (3:4) параллельно касательной к кривой y=x^2 в точке, абсцисса которой равна 3.

Answer 1

Находим уравнение касательной в точке х = 3.
y' = 2x,
y'(3) = 2*3 = 6,
y(3) = 3² = 9.
yk = 6(x-3)+9 = 6x - 18 + 9 = 6x - 9.
Теперь можно найти уравнение параллельной линии, проходящей через точку (3; 4) в виде у = кх + в, к = 6 по уравнению касательной.
4 = 6*3 + в,
в = 4 - 18 = -14.

Ответ: у = 6х - 14.