Question

В треугольникн abc на стороне ac взята точка k, ak=kc=bk, угол akb на 60° больше угла c. Найдите угол abk. Только напишите доказательство

Answer 1

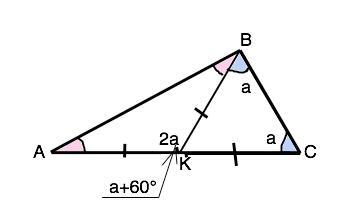
По условию АК=СК=ВК ⇒  Отрезок ВК - медиана АВС и равна АС:2. Поэтому треугольники АВК и СВК - равнобедренные, углы при АС и при ВС равны.  Примем ∠КСВ=∠СВК=а. Тогда внешний угол при вершине К треугольника СВК угол АКВ=2а=а+60°, поэтому ∠КВС=∠СВК=60°, а ∠АКВ=120°. В равнобедренном ∆ АКВ ∠ВАК=∠АВК=(180°-120°):2=30°