Question

Найдите радиус окружности, если расстояние от центра окружности до хорды равно 9см, а длина хорды равно 24 см

Answer 1

Расстояние от центра до хорды - перпендикуляр, делящий хорду на две равные части(24:2=12). Вследствии этого образуется прямоугольный треугольник, где радиус является гипотенузой. По Теореме Пифагора следует
r^2=9^2+12^
r^2=81+144=225
r=√225=15 см - ответ

Answer 2

Ответ:    15 см

Объяснение:

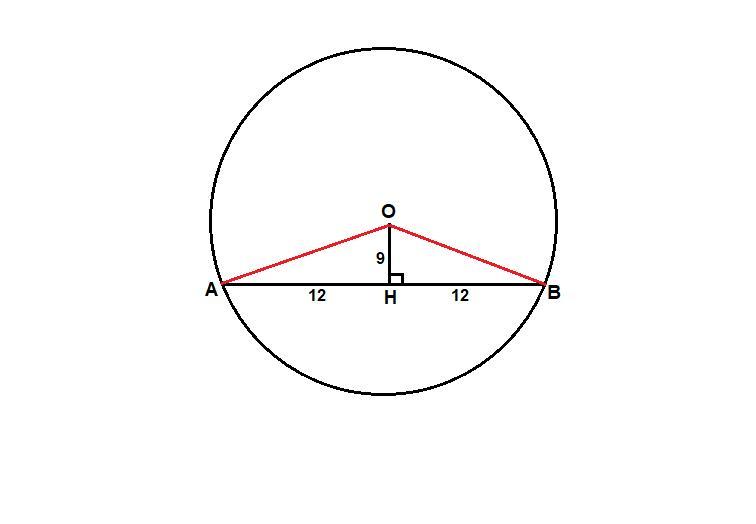
АВ - хорда, О - центр окружности.

Расстояние от центра окружности до хорды - это длина перпендикуляра, проведенного из центра к хорде - ОН = 9 см.

Треугольник АОВ равнобедренный, так как ОА = ОВ как радиусы.

Тогда ОН - его высота и медиана.

АН = АВ/2 = 12 см

ΔАОН:   ∠АНО = 90°, по теореме Пифагора

            ОА = √(АН² + ОН²) = √(12² + 9²) = √(144 + 81) = √225 = 15 см

Answer 3

Ответ:

решение представлено на фото

Объяснение: