Дана окружность с центром в точке O радиуса 15 и точка P такая, что OP=37.через точку P проведена прямая,пересекающая окружность в точках A и B таких,что AB=18.найдите длину отрезка BP.
Ответы
Ответ дал:
0
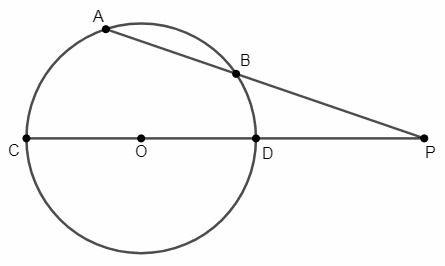
CD - диаметр, D∈OP
OC=OD=15, OP=37, AB=18
Из точки вне окружности (P) проведены две секущие (PA, PC). Произведение одной секущей на её внешнюю часть равно произведению другой секущей на её внешнюю часть (теорема о секущих).
PA*PB=PC*PD
PA=AB+BP =18+BP
PC=OC+OP =15+37 =52
PD=OP-OD =37-15 =22
(18+BP)BP=52*22 <=>
BP^2 +18BP -1144 =0 <=>
BP1,2= -9 +- √(81+1144) =
=35-9 =26 (BP>0)
OC=OD=15, OP=37, AB=18
Из точки вне окружности (P) проведены две секущие (PA, PC). Произведение одной секущей на её внешнюю часть равно произведению другой секущей на её внешнюю часть (теорема о секущих).
PA*PB=PC*PD
PA=AB+BP =18+BP
PC=OC+OP =15+37 =52
PD=OP-OD =37-15 =22
(18+BP)BP=52*22 <=>
BP^2 +18BP -1144 =0 <=>
BP1,2= -9 +- √(81+1144) =
=35-9 =26 (BP>0)
Приложения:
Вас заинтересует
2 года назад
3 года назад
3 года назад
9 лет назад
10 лет назад
10 лет назад