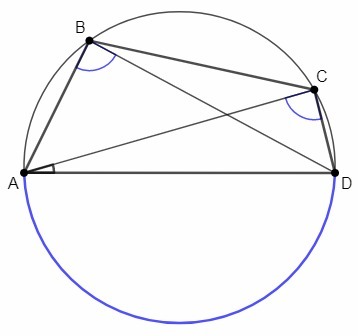
Четырехугольник АВСD, вписан в окружность. Угол АВD равен 88 градусов, угол САD равен 16гоадусов. Найдите угол АDС. Ответ дайте в градусах.
Ответы
Ответ дал:
0
Все углы вписанные, значит дуги на которые они опираются равны 2*градусную меру угла.
Угол adc=0.5 дуги на которую он опирается, =(360-2*88-2*16)/2=76
Угол adc=0.5 дуги на которую он опирается, =(360-2*88-2*16)/2=76
Ответ дал:
0
∠ABD=88°, ∠CAD=16°
Вписанные углы, опирающиеся на одну дугу, равны.
∠ACD=∠ABD =88° (=∪AD/2)
Сумма углов треугольника 180°
△ACD: ∠ADC=180° -∠CAD -∠ACD =180°-16°-88° =76°
Вписанные углы, опирающиеся на одну дугу, равны.
∠ACD=∠ABD =88° (=∪AD/2)
Сумма углов треугольника 180°
△ACD: ∠ADC=180° -∠CAD -∠ACD =180°-16°-88° =76°
Приложения:
Вас заинтересует
2 года назад
2 года назад
3 года назад
3 года назад
9 лет назад
10 лет назад