Найти частное решение, удовлетворяющее начальным условиям ( Линейные уравнения первого порядка)
Приложения:
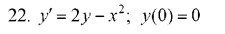
Ответы
Ответ дал:
0
y' - 2y = -x²
решаем однородное:
y' - 2y = 0
y' = 2y
dy/y = 2dx
lny - lnC = 2x
y = C*e^{2x}
решение ищем в виде: y = C(x) * e^{2x}
C'(x) * e^{2x} + 2C(x) * e^{2x} - 2C(x) * e^{2x} + x² = 0
C'(x) = -x²*e^{-2x}
C(x) = -∫x²e^{-2x}dx = 0,5∫x²d(e^{-2x}) = 0,5x²e^{-2x} - ∫xe^{-2x}dx = 0,5x²e^{-2x} + 0,5∫xd(e^{-2x}) = 0,5x²e^{-2x} + 0,5xe^{-2x} - 0,5∫e^{-2x}dx = 0,5e^{-2x}(x² + x +0,5) + C1
y = 0,5(x² + x + 0,5) + C1*e^{2x}
y(0) = 0,25 + C1 = 0 => C1 = -0,25
y = 0,5(x² + x + 0,5) -0,25e^{2x}
решаем однородное:
y' - 2y = 0
y' = 2y
dy/y = 2dx
lny - lnC = 2x
y = C*e^{2x}
решение ищем в виде: y = C(x) * e^{2x}
C'(x) * e^{2x} + 2C(x) * e^{2x} - 2C(x) * e^{2x} + x² = 0
C'(x) = -x²*e^{-2x}
C(x) = -∫x²e^{-2x}dx = 0,5∫x²d(e^{-2x}) = 0,5x²e^{-2x} - ∫xe^{-2x}dx = 0,5x²e^{-2x} + 0,5∫xd(e^{-2x}) = 0,5x²e^{-2x} + 0,5xe^{-2x} - 0,5∫e^{-2x}dx = 0,5e^{-2x}(x² + x +0,5) + C1
y = 0,5(x² + x + 0,5) + C1*e^{2x}
y(0) = 0,25 + C1 = 0 => C1 = -0,25
y = 0,5(x² + x + 0,5) -0,25e^{2x}
Ответ дал:
0
ну вот еще 49 бал, ваш акаунт слишком старнный !
Вас заинтересует
2 года назад
3 года назад
3 года назад
9 лет назад
9 лет назад
10 лет назад
10 лет назад