Question

Прямая линия заданная уравнением линейной функции ax-3y=4 проходит через точку пересечения прямых x-y=7 и x+y=-3 Найдите значение а

Answer 1

Находим точку пересечения прямых x-y=7 и x+y=-3 путём решения системы:
{x-y=7
{x+y=-3.
Сложим уравнения:
{x-y=7
{x+y=-3.
-----------
2х = 4,
х = 4/2 = 2,   у = х - 7 = 2 - 7 = -5.
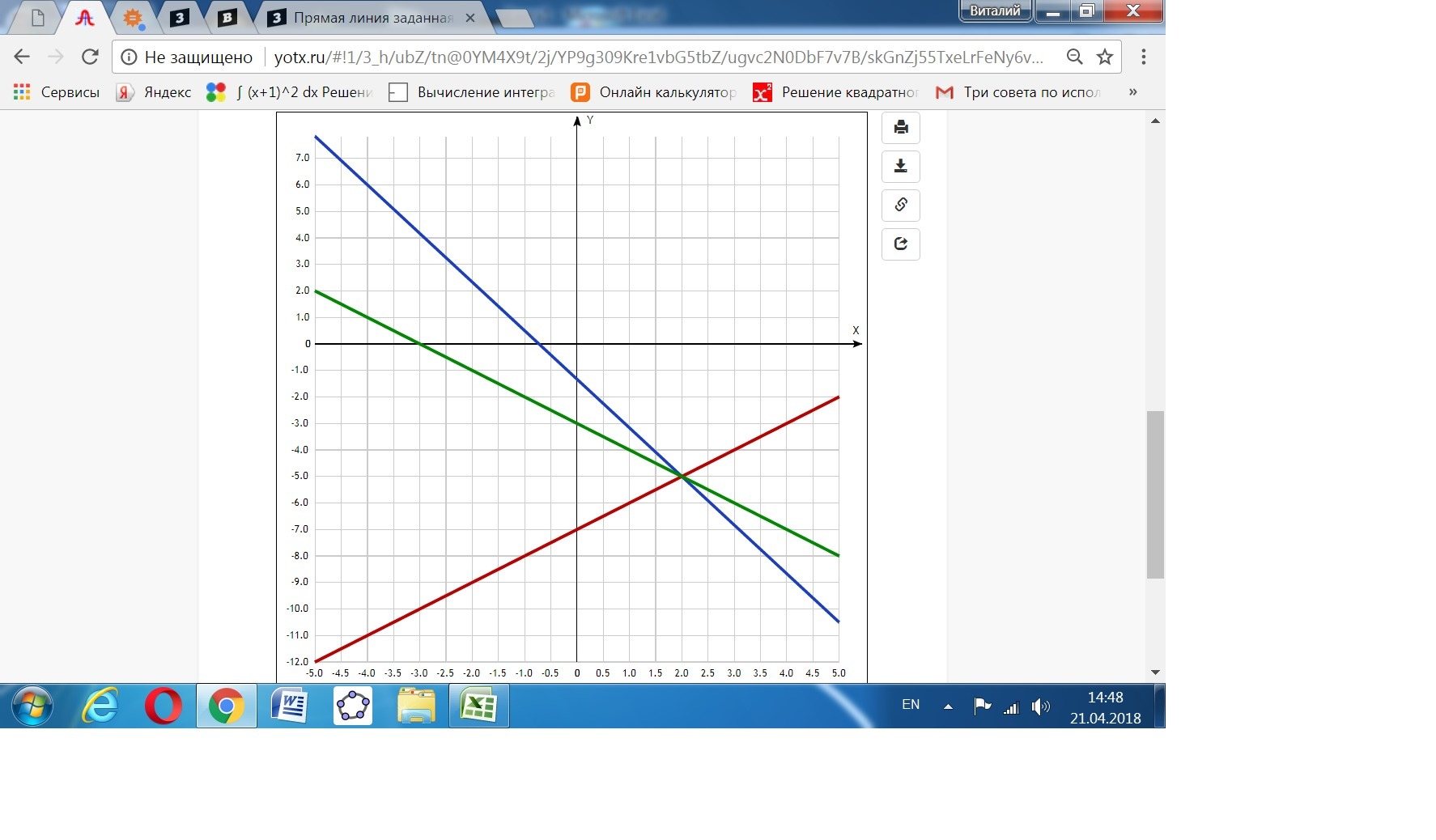
Точка пересечения имеет координаты (2; -5).

Значение а находим из заданного уравнения ax-3y=4, подставив в него координаты х и у точки пересечения.
а = (4 + 3у)/х = (4+3*(-5))/2 = (4 - 15)/2 = -5,5.