Ответы
Ответ дал:
0
Ответ дал:
0
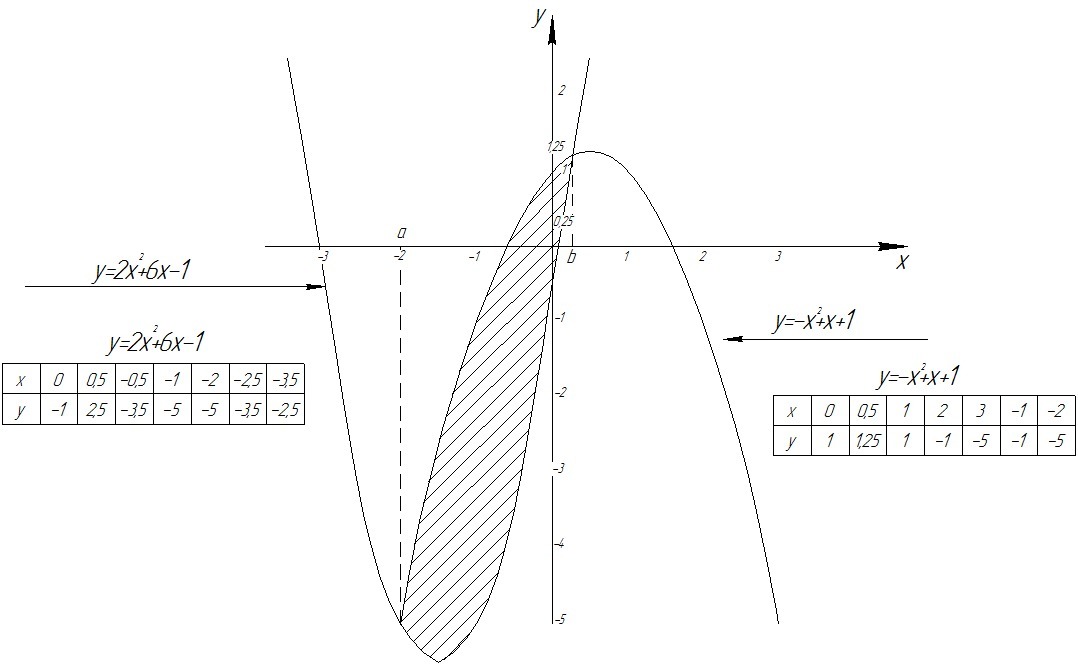
Найдем абсциссы точек пересечения заданных линий:

 - пределы интегрирования. (на рисунке изображены как "a" и "b".
- пределы интегрирования. (на рисунке изображены как "a" и "b".


Приложения:
Вас заинтересует
3 года назад
9 лет назад
9 лет назад
10 лет назад
10 лет назад