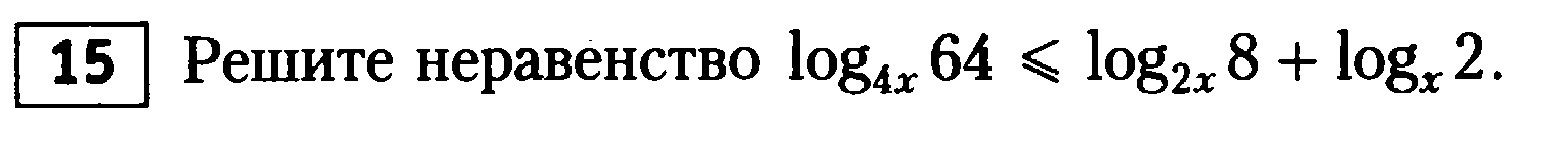Ответы
Ответ дал:
0
ОДЗ: ![displaystylemathtt{left{{{x textgreater 0}atop{xneq(frac{1}{2})^n,~nin[0;2]}}right} displaystylemathtt{left{{{x textgreater 0}atop{xneq(frac{1}{2})^n,~nin[0;2]}}right}](https://tex.z-dn.net/?f=displaystylemathtt%7Bleft%7B%7B%7Bx+textgreater++0%7Datop%7Bxneq%28frac%7B1%7D%7B2%7D%29%5En%2C%7Enin%5B0%3B2%5D%7D%7Dright%7D)
изобразим неравенство слегка иначе:
дальше – больше! сплошные выносы степеней и оснований логарифмов с последующей заменой :
:

решение неравенства с заменой:![mathtt{ain(infty;-2)U(-1;-frac{1}{2}]U(0;2]} mathtt{ain(infty;-2)U(-1;-frac{1}{2}]U(0;2]}](https://tex.z-dn.net/?f=mathtt%7Bain%28infty%3B-2%29U%28-1%3B-frac%7B1%7D%7B2%7D%5DU%280%3B2%5D%7D)
обратная замена:
учитывая ОДЗ, получаем окончательный ответ:![mathtt{xin(0;frac{1}{4})U(frac{1}{2};frac{sqrt{2}}{2}]U(1;4]} mathtt{xin(0;frac{1}{4})U(frac{1}{2};frac{sqrt{2}}{2}]U(1;4]}](https://tex.z-dn.net/?f=mathtt%7Bxin%280%3Bfrac%7B1%7D%7B4%7D%29U%28frac%7B1%7D%7B2%7D%3Bfrac%7Bsqrt%7B2%7D%7D%7B2%7D%5DU%281%3B4%5D%7D)
изобразим неравенство слегка иначе:
дальше – больше! сплошные выносы степеней и оснований логарифмов с последующей заменой
решение неравенства с заменой:
обратная замена:
учитывая ОДЗ, получаем окончательный ответ:
Вас заинтересует
2 года назад
3 года назад
3 года назад
9 лет назад
10 лет назад