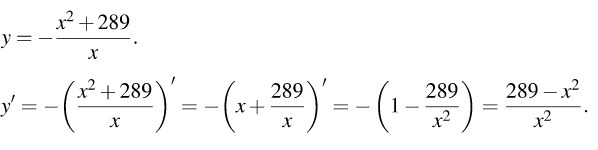Ответы
Ответ дал:
0
по формулам:
![1) [u+v]'=u'+v'\\
2) (x^a)'=a*x^{a-1}\\
(x)'=(x^1)=1*x^{1-1}=1*x^0=1*1=1\\
(frac{1}{x})'=(x^{-1})'=-1*x^{-1-1}=-x^{-2}=-frac{1}{x^2}\\
3) [c*f(x)]'=c*[f(x)]'=c*f'(x)\\
------------------------------\\
(frac{289}{x})'=(289*frac{1}{x})'=289*(frac{1}{x})'=289*(-frac{1}{x^2})=-frac{289}{x^2}\\
y(x)=-frac{x^2+289}{x}=-(frac{x^2}{x}+frac{289}{x})=-(x+frac{289}{x})=(-1)*(x+frac{289}{x})\\
y'(x)=[(-1)*(x+frac{289}{x})]'=(-1)*[x+frac{289}{x}]'=\\](https://tex.z-dn.net/?f=1%29++%5Bu%2Bv%5D%27%3Du%27%2Bv%27%5C%5C%0A2%29++%28x%5Ea%29%27%3Da%2Ax%5E%7Ba-1%7D%5C%5C%0A%28x%29%27%3D%28x%5E1%29%3D1%2Ax%5E%7B1-1%7D%3D1%2Ax%5E0%3D1%2A1%3D1%5C%5C%0A%28frac%7B1%7D%7Bx%7D%29%27%3D%28x%5E%7B-1%7D%29%27%3D-1%2Ax%5E%7B-1-1%7D%3D-x%5E%7B-2%7D%3D-frac%7B1%7D%7Bx%5E2%7D%5C%5C%0A3%29++%5Bc%2Af%28x%29%5D%27%3Dc%2A%5Bf%28x%29%5D%27%3Dc%2Af%27%28x%29%5C%5C%0A------------------------------%5C%5C%0A%28frac%7B289%7D%7Bx%7D%29%27%3D%28289%2Afrac%7B1%7D%7Bx%7D%29%27%3D289%2A%28frac%7B1%7D%7Bx%7D%29%27%3D289%2A%28-frac%7B1%7D%7Bx%5E2%7D%29%3D-frac%7B289%7D%7Bx%5E2%7D%5C%5C%0Ay%28x%29%3D-frac%7Bx%5E2%2B289%7D%7Bx%7D%3D-%28frac%7Bx%5E2%7D%7Bx%7D%2Bfrac%7B289%7D%7Bx%7D%29%3D-%28x%2Bfrac%7B289%7D%7Bx%7D%29%3D%28-1%29%2A%28x%2Bfrac%7B289%7D%7Bx%7D%29%5C%5C%0Ay%27%28x%29%3D%5B%28-1%29%2A%28x%2Bfrac%7B289%7D%7Bx%7D%29%5D%27%3D%28-1%29%2A%5Bx%2Bfrac%7B289%7D%7Bx%7D%5D%27%3D%5C%5C "1) [u+v]'=u'+v'\\
2) (x^a)'=a*x^{a-1}\\
(x)'=(x^1)=1*x^{1-1}=1*x^0=1*1=1\\
(frac{1}{x})'=(x^{-1})'=-1*x^{-1-1}=-x^{-2}=-frac{1}{x^2}\\
3) [c*f(x)]'=c*[f(x)]'=c*f'(x)\\
------------------------------\\
(frac{289}{x})'=(289*frac{1}{x})'=289*(frac{1}{x})'=289*(-frac{1}{x^2})=-frac{289}{x^2}\\
y(x)=-frac{x^2+289}{x}=-(frac{x^2}{x}+frac{289}{x})=-(x+frac{289}{x})=(-1)*(x+frac{289}{x})\\
y'(x)=[(-1)*(x+frac{289}{x})]'=(-1)*[x+frac{289}{x}]'=\\")
![=-[(x)'+(frac{289}{x})']=-[1+(-frac{289}{x^2})]=\\
=-[1-frac{289}{x^2}]=-[frac{x^2}{x^2}-frac{289}{x^2}]=-[frac{x^2-289}{x^2}]=-frac{x^2-289}{x^2}=\\
=frac{-(x^2-289)}{x^2}=frac{-x^2+289}{x^2}=frac{289-x^2}{x^2}](https://tex.z-dn.net/?f=%3D-%5B%28x%29%27%2B%28frac%7B289%7D%7Bx%7D%29%27%5D%3D-%5B1%2B%28-frac%7B289%7D%7Bx%5E2%7D%29%5D%3D%5C%5C%0A%3D-%5B1-frac%7B289%7D%7Bx%5E2%7D%5D%3D-%5Bfrac%7Bx%5E2%7D%7Bx%5E2%7D-frac%7B289%7D%7Bx%5E2%7D%5D%3D-%5Bfrac%7Bx%5E2-289%7D%7Bx%5E2%7D%5D%3D-frac%7Bx%5E2-289%7D%7Bx%5E2%7D%3D%5C%5C%0A%3Dfrac%7B-%28x%5E2-289%29%7D%7Bx%5E2%7D%3Dfrac%7B-x%5E2%2B289%7D%7Bx%5E2%7D%3Dfrac%7B289-x%5E2%7D%7Bx%5E2%7D "=-[(x)'+(frac{289}{x})']=-[1+(-frac{289}{x^2})]=\\
=-[1-frac{289}{x^2}]=-[frac{x^2}{x^2}-frac{289}{x^2}]=-[frac{x^2-289}{x^2}]=-frac{x^2-289}{x^2}=\\
=frac{-(x^2-289)}{x^2}=frac{-x^2+289}{x^2}=frac{289-x^2}{x^2}")
Вас заинтересует
2 года назад
3 года назад
9 лет назад