Неопределенный интеграл метод замены. Номер 61 под цифрой 3,4. Буду благодарен даже одному решенному заданию
Приложения:
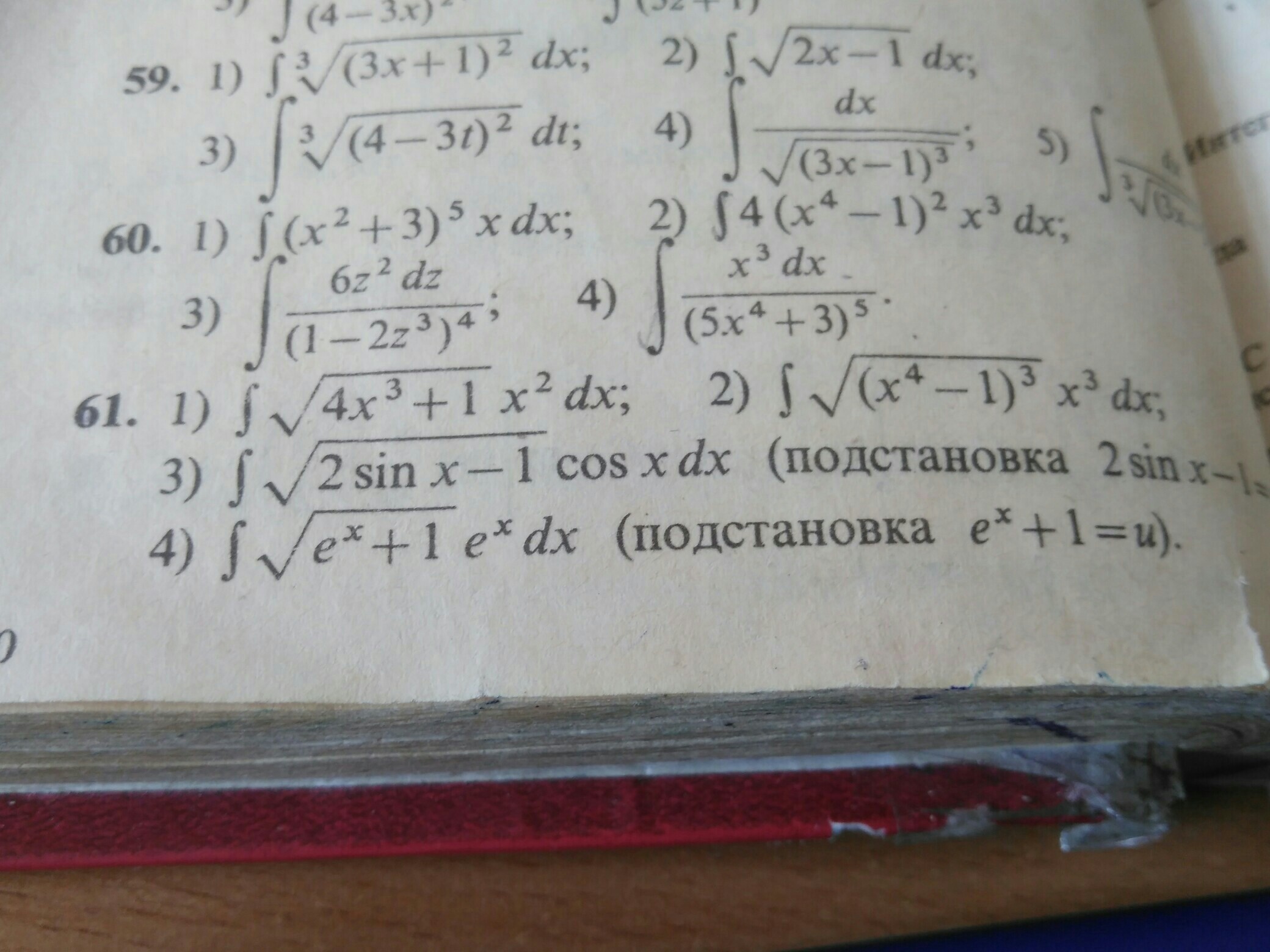
Ответы
Ответ дал:
0
Вас заинтересует
2 года назад
2 года назад
3 года назад
3 года назад
9 лет назад
9 лет назад
10 лет назад