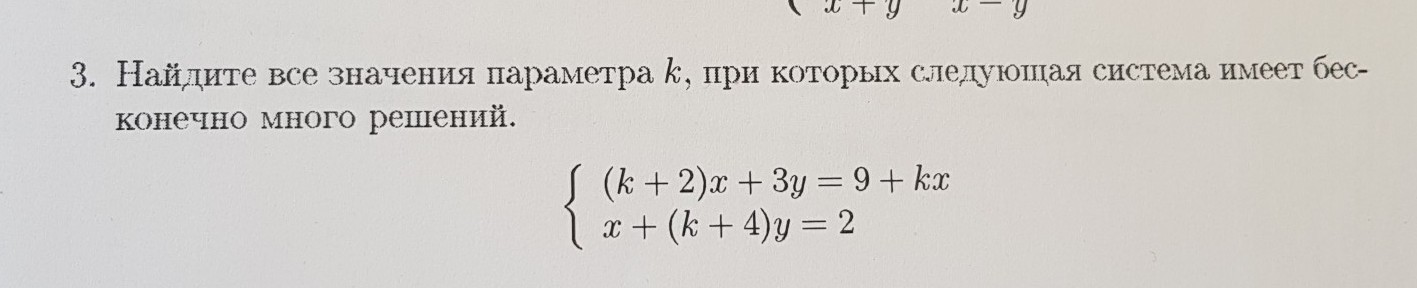Question

Очень прошу помочь, не понимаю тему!!! Много баллов за один пример!!!

Answer 1

$y(x)=kx+b$ - график - прямая линия, коэффициент $k$ задает угол наклона этой линии к оси OX

коэффициент $b$ поднимает / опускает график (параллельным переносом) вдоль оси ОУ

если есть две прямые:
$y_1(x)=k_1x+b_1\\ y_2(x)=k_2x+b_2$,

если у этих двух прямых коэффициенты равны $k_1=k_2$, то это означает, что углы наклона к оси OX у этих прямых совпадаю, из чего следует, что эти две прямые либо параллельны либо накладываються.

если дополнительно потребовать, что бы $b_1=b_2$, то прямые $y_1$ и  $y_2$ будут не просто параллельны, а будут обязательно накладываться, что будет означать что система уравнений
$left { {{y=k_1x+b_1} atop {y=k_2x+b_2}} right.$  иметь бесконечное количество решений

---------------------------

прямая линия задана уравненим:
$ax+by+c=0$, если $b neq$, то
$by=-ax-c\\ y=-frac{a}{b}x-frac{c}{b}\\ y=k'x+b'$
где $k'=-frac{a}{b}\\ b'=-frac{c}{b}$

это означает, что система уравнений:
$left { {{a_1x+b_1y+c_1=0} atop {a_2x+b_2y+c_2=0}} right.$
будет иметь бессконечное количество решений при выполнении системы условий:
$left { {{frac{a_1}{b_1}=frac{a_2}{b_2}} atop {frac{c_1}{b_1}=frac{c_2}{b_2}}} right. \\ left { {{frac{a_1}{a_2}=frac{b_1}{b_2}} atop {frac{c_1}{c_2}=frac{b_1}{b_2}}} right. \\ {frac{a_1}{a_2}=frac{b_1}{b_2}=frac{c_1}{c_2}$

--------------------------------------
$left { {{(k+2)x+3y=9+kx} atop {x+(k+4)y=2}} right. \\ left { {{(k+2)x-kx+3y-9=0} atop {x+(k+4)y-2=0}} right. \\ left { {{(k+2-k)x+3y-9=0} atop {x+(k+4)y-2=0}} right. \\ left { {{2*x+3*y-9=0} atop {1*x+(k+4)*y-2=0}} right.$

необходимое и достаточное условие $frac{2}{1}=frac{3}{k+4}=frac{-9}{-2}$ для параллельности прямых не выполняеться, по скольку $frac{2}{1}neq frac{-9}{-2}$
------------------------------
Ответ: таких значений для $k$ не существует, что бы указанная система имела бесконечное количество решений

Answer 2

2k+5

Answer 3

при условии k=-2.5

Answer 4

тогда система выглядит как: 2x+3y-9=0 и x+1.5y-2=0

Answer 5

или как 2x+3y-9=0 и 2x+3y-4=0 - эти прямые, конечно же параллельны

Answer 6

т.е. СЛАУ решений не имеет