Question

Основания трапеции относятся как 2:3, а ее площадь равна 50 см2. Найти площади:

а) двух треугольников, на которые данная трапеция делится диагональю

б) четырех треугольников, на которые данная трапеция делится диагоналями.

Answer 1

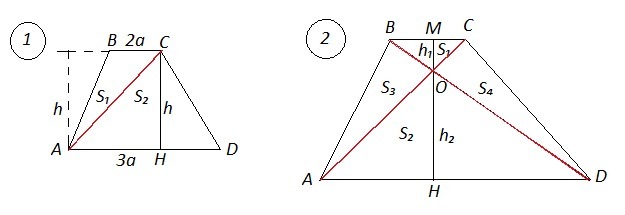
1)  Трапеция ABCD.  По условию  BC:AD=2:3  ⇒  BC=2a  ,  AD=3a .
     S(ABCD)=50 см² .
   h=CH⊥AD ,  h - высота не только трапеции, но и ΔACD и ΔАВС.
  S(ABCD)=S(ABC)+S(ACD)=S₁+S₂ =1/2*2a*h+1/2*3a*h=
                 =1/2*h(2a+3a)=1/2*h*5a=5/2*ah
            50=5/2*ah  ⇒  ah=50:5/2=20
          S₁=1/2*2ah=ah=20  ,  S₂=1/2*3a*h=3/2*ah=3/2*20=30
2)  ВС=2а  ,  AD=3a  ,  h=MH⊥AD,  h₁=OM ,  h₂=OH ,  h=h₁+h₂ .
      
$S(ABCD)=S(BOC)+S(AOD)+S(AOB)+S(COD)=\\=S_1+S_2+S_3+S_4\\S_1=frac{1}{2}cdot 2ah_2; ,; ; S_2=frac{1}{2}cdot 3ah_2\\S_3=S(ABD)-S(AOD)=frac{1}{2}cdot 3ah-frac{1}{2}cdot 3ah_2\\S_4=S(ACD)-S(AOD)=frac{1}{2}cdot 3ah-frac{1}{2}3ah_2\\S_3=S_4\\S_3+S_4=2cdot (frac{1}{2}cdot 3ah-frac{1}{2}cdot 3ah_2)=3ah-3ah_2=60-3ah_2$
  
Из пункта №1:  3ah=3*20=60

$S(ABCD)=S_1+S_2+S_3+S_4=\\=frac{1}{2}cdot 2ah_1+frac{1}{2}cdot 3ah_2+60-3ah_2=ah_1+60-frac{3}{2}cdot ah_2=\\=acdot (h-h_2)+60-frac{3}{2}ah_2=ah-ah_2+60-frac{3}{2}ah_2=\\=20+60-frac{5}{2}ah_2=80-frac{5}{2}ah_2\\50=80-frac{5}{2}ah_2\\frac{5}{2}ah_2=30; ,; ; ah_2=12\\S_2=frac{3}{2}cdot ah_2=frac{3}{2}cdot 12=18\\50=ah_1+60-frac{3}{2}cdot ah_2; ,; 50=ah_1+60-18,\\50=ah_1+42; ,; ; ah_1=8\\S_1=frac{1}{2}cdot 2ah_1=ah_1=8\\S_3=S_4=frac{1}{2}cdot (60- 3ah_2)=frac{1}{2}(60-3cdot 12)=12$