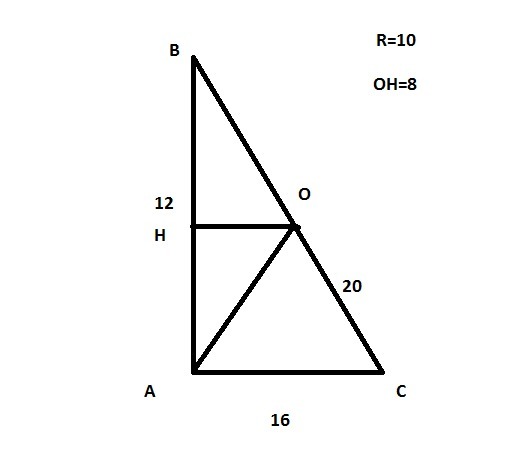
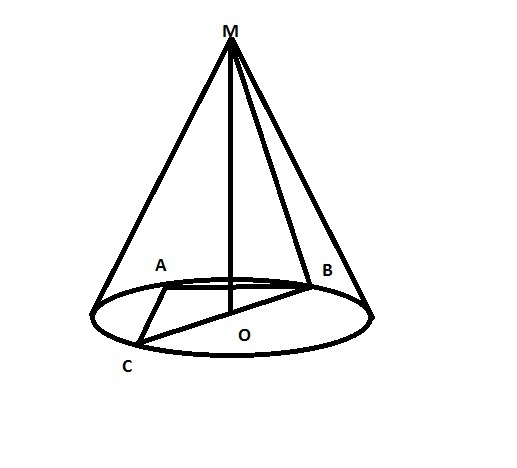
В конус вписана пирамида МАВС, основанием которой служит прямоугольный треугольник с катетами АВ=12 и ВС=16. Двугранный угол при катете ВС равен 60 градусов. Найдите площадь грани МВС и площадь боковой поверхности конуса.
Ответы
Ответ дал:
0
высота пирамиды h=OH/cos60=16=OM
MH=√(16^2+8^2)=√320=8√5
S(MBC)=BC*MH/2=12*8√5/2=48√5
Образующая конуса совпадет с боковым ребром пирамиды
BM=√(R^2+OM^2)=√(10^2+16^2=√356=4√21
S(бок)=pi*10*4√21=40pi√21
MH=√(16^2+8^2)=√320=8√5
S(MBC)=BC*MH/2=12*8√5/2=48√5
Образующая конуса совпадет с боковым ребром пирамиды
BM=√(R^2+OM^2)=√(10^2+16^2=√356=4√21
S(бок)=pi*10*4√21=40pi√21
Приложения:
Вас заинтересует
2 года назад
2 года назад
2 года назад
8 лет назад
8 лет назад
9 лет назад