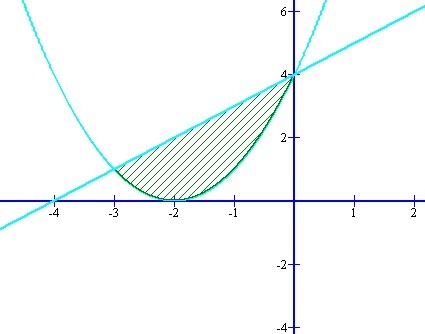
Срочно! 11 класс Найдите площадь фигуры, ограниченной параболой y = x^2 + 4x + 4 и прямой y = x + 4
Ответы
Ответ дал:
0
Площадь:
Приложения:
Вас заинтересует
2 года назад
2 года назад
3 года назад
9 лет назад
10 лет назад