Question

РЕШИТЕ СРОЧНО!!!
№1
Составьте уравнение касатаельной к графику функции
y=x^6 +4x^3 - 1 в точке с абсциссой х=-1.
№2
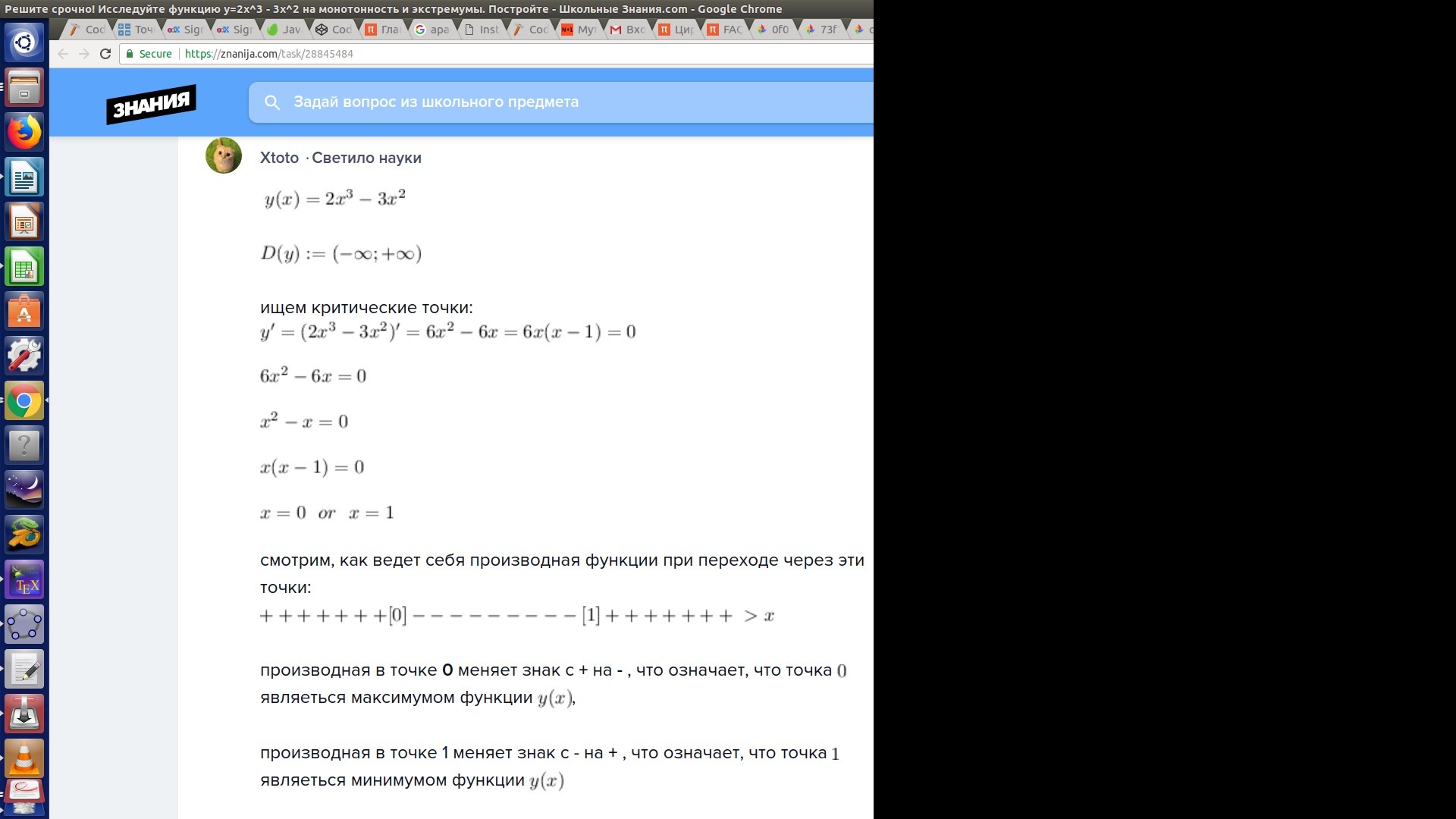
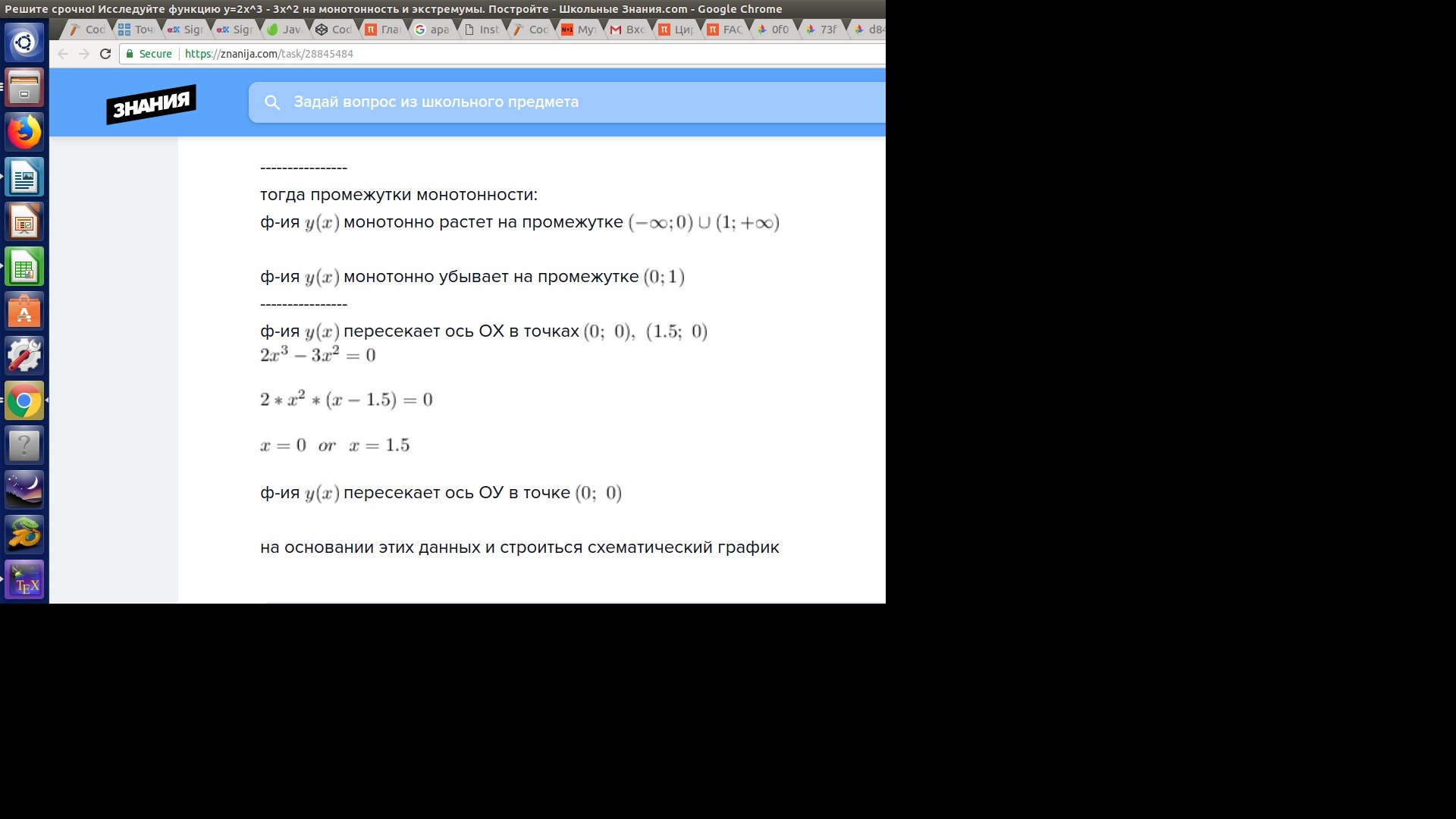
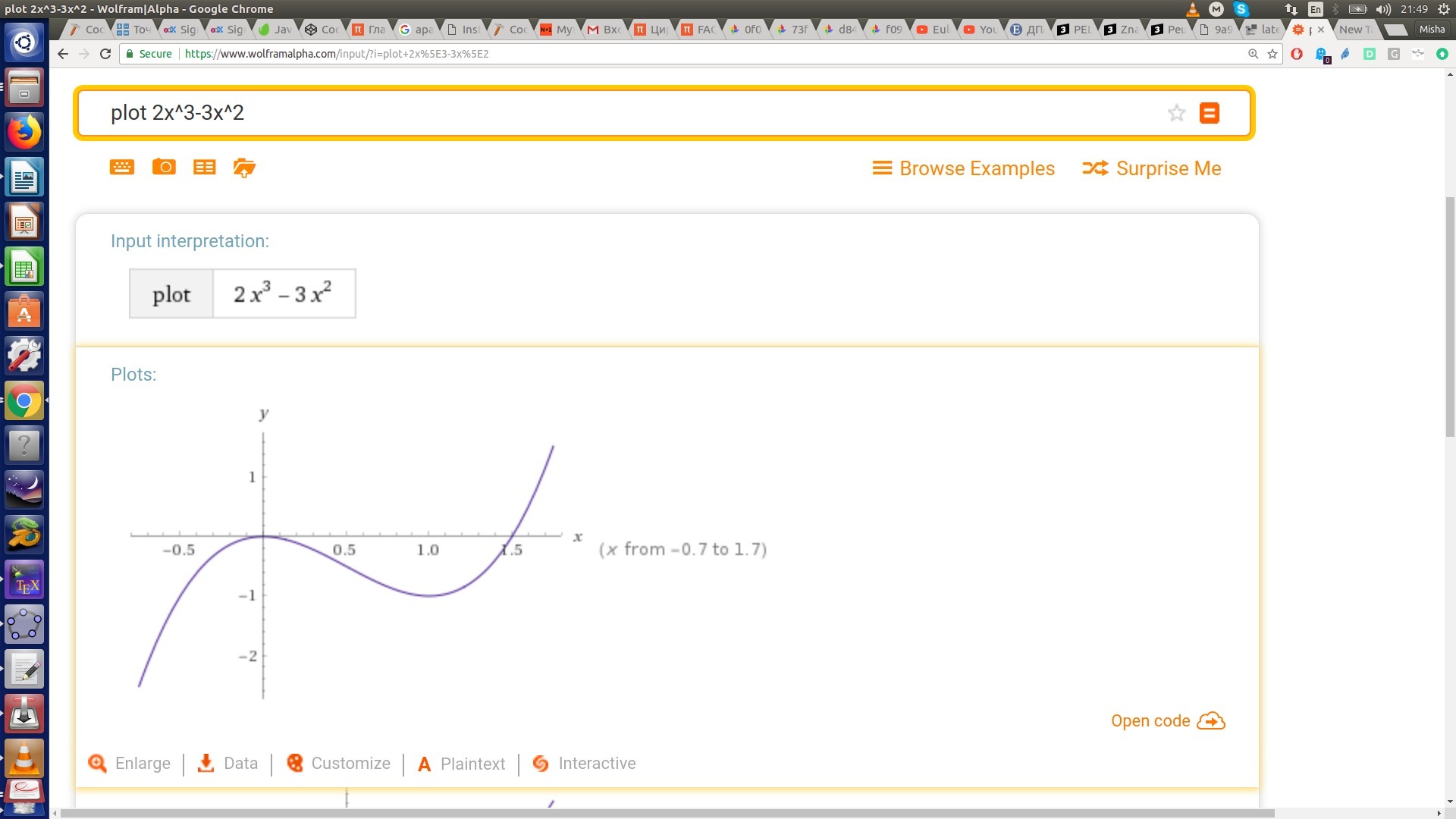
Исследуйте функцию y=x^3 - 3x^2 на монотонность и экстремумы и постройте её график.
№3
Тупой или острый угол образует с положительным направлением оси х касательная к графику функции
у= под корнем 5-4x,проведённая в точке с абсциссой х=1 ?.

Answer 1

$L(x)=f(a)+f'(a)(x-a)$ - уравнение касательной к функции $f(x)$ в точке $x=a$

1)
$f'(x)=[x^6+4x^3-1]'=6x^5+12x^2\\ f'(-1)=-6+12=6\\ f(-1)=1-4-1=-4\\ L(x)=-4+6*(x-(-1))=-4+6(x+1) =-4+6x+6=\\=L(x)=6x+2$

3)
$f(x)=sqrt{5-4x}\\ f'(x)=frac{(5-4x)'}{2sqrt{5-4x}}=frac{-4}{2sqrt{5-4x}}=-frac{2}{sqrt{5-4x}}\\ f(1)=sqrt{5-4}=1\\ f'(1)=-frac{2}{1}=-2\\ L(x)=1+(-2)*(x-1)=1-2x+2=-2x+3\\ tg(alpha)=-2 textless 0$


2) - скриншотами своего же решения ранее
тупой угол