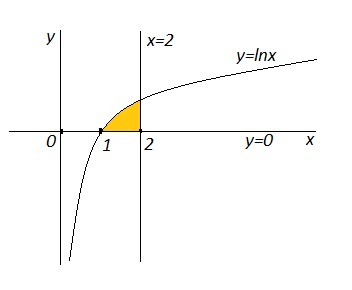
Фигура ограничена линиями y=lnx x=2 y=0. Найти объём тела образованного вращением этой фигуры вокруг оси OX
Ответы
Ответ дал:
0
Приложения:
Вас заинтересует
2 года назад
3 года назад
3 года назад
9 лет назад
9 лет назад
10 лет назад
10 лет назад