Заданы математическое ожидание a и среднее квадратич-
ное отклонение σ нормально распределенной случайной величины X . На-
писать плотность распределения вероятностей . Найти вероятность того, что X примет значение из интервала
(α,β)
Приложения:
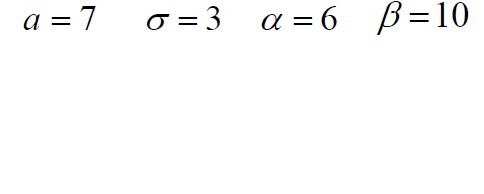
Ответы
Ответ дал:
0
Непрерывная случайная величина X, распределённая по нормальному закону, имеет функцию плотности:

В нашем случае: а=7, σ=3

Вероятность попадания Х в интервал (α,β):

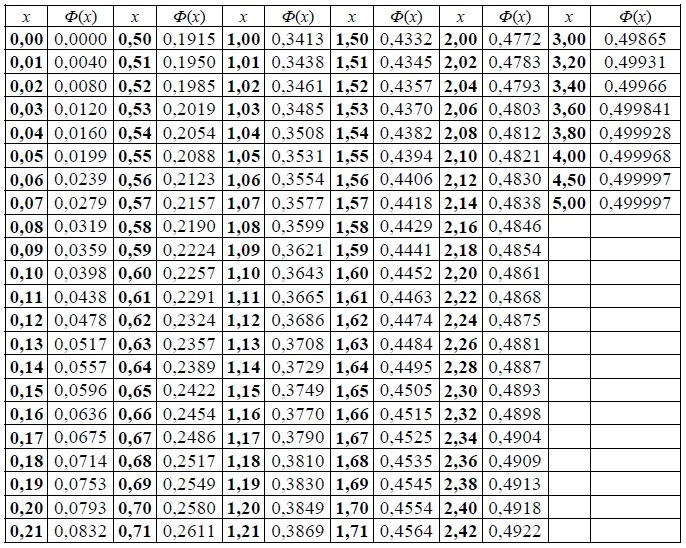
Где Ф(x) - функция Лапласа (табличное значение)

Функция Лапласа нечетная, значит: Ф(-x)=-Ф(х), поэтому


В нашем случае: а=7, σ=3
Вероятность попадания Х в интервал (α,β):
Где Ф(x) - функция Лапласа (табличное значение)
Функция Лапласа нечетная, значит: Ф(-x)=-Ф(х), поэтому
Приложения:

Вас заинтересует
2 года назад
2 года назад
3 года назад
3 года назад
9 лет назад
9 лет назад
10 лет назад
10 лет назад