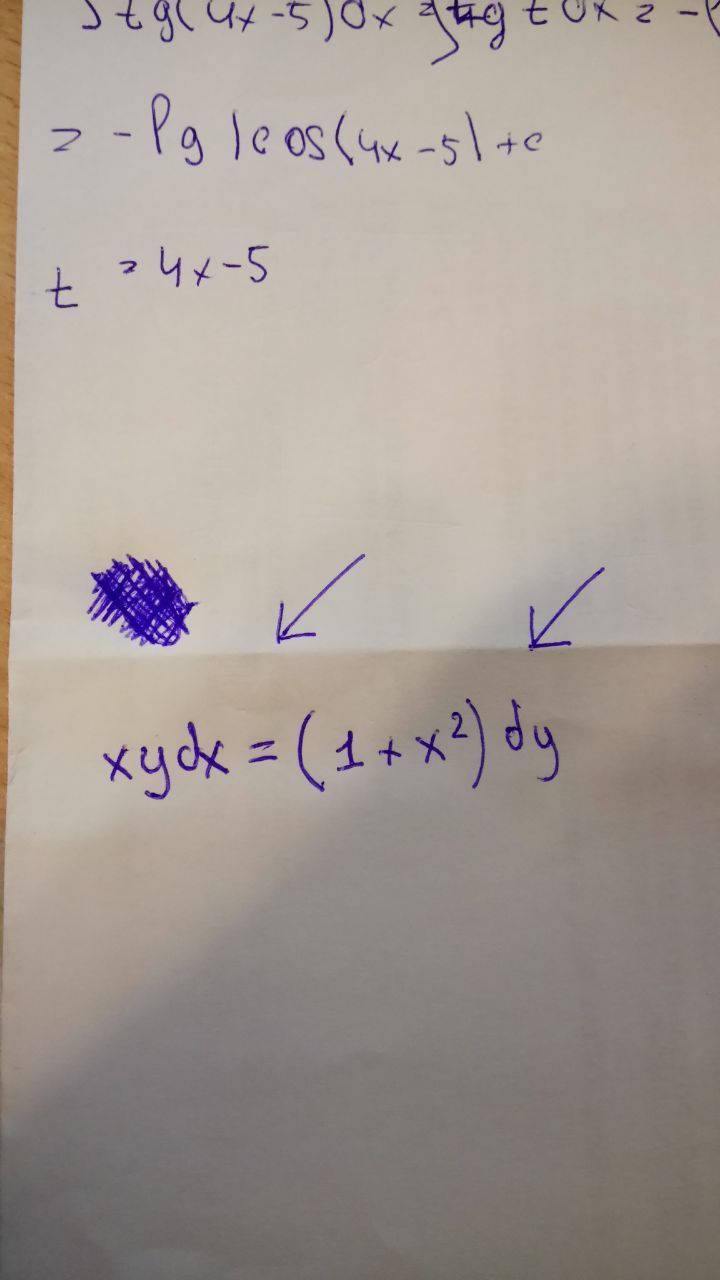Ответы
Ответ дал:
0
Частное решение у=0 получаемое при делении на у, входит в общее при С*=0
Вас заинтересует
2 года назад
2 года назад
3 года назад
3 года назад
9 лет назад
10 лет назад