Question

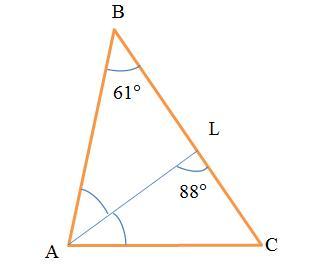
в треугольнике abc проведена биссектриса al угол alc равен 88 угол abc равен 61 найдите угол acb ответ лайте в градусах

Answer 1

Угол
ALB=180-112=68,
тогда угол BAL=180-106-68=6, так как AL- биссектриса, угол BAC=6+6=12 поэтому ACB=180-106-12=62

Answer 2

Ответ:

∠ACB = 65°

Объяснение:

Дано:

В ΔABC (см. рисунок)

∠ABC=∠ABL=61°

∠ALC=88°  

Найти: ∠ACB

Решение.

Так как ∠ALC=88°, то смежный с ним угол ∠ALB=180° - 88° = 92°.  

Используем свойство: сумма внутренних углов треугольника равна 180°: ∠АLB+∠АBL+∠BАL=180°

Отсюда:

∠BAL = 180° - ∠ALB - ∠АBL = 180° - 92° - 61° = 27°.

Биссектриса делит ∠BАC пополам, то

∠BАC = 2·∠BAL = 2·27° = 54°.

Ещё раз используем свойство: сумма внутренних углов треугольника равна 180°: ∠BАC+∠АBC+∠АCB=180°

Отсюда:

∠ACB = 180° - ∠BАC - ∠АBC = 180° - 54° - 61° = 65°.

Ответ: ∠ACB = 65°.