Question

1.Решить дифференциальное уравнение: y^2dx=(xy-x^2)dy
2.решить двойной интеграл:
Двойной интеграл e^xdxdy, D: y=lnx, y=0, x=2
Помогите пожалуйста T_T

Answer 1

1) y^2 dx = (xy - x^2) dy
y^2 dx = xy dy - x^2 dy – раскрыли скобки
y (y dx - x dy) = -x^2 dy – перенесли слагаемое в другую часть, вынесли y за скобку
-y d(y/x) = -dy – разделим на x^2, получим полный дифференциал y/x. !!! Могло потеряться решение x = 0.
-d(y/x) = -dy/y – делим на y. !!! Могло потеряться решение y = 0.
d(y/x) - d(ln Cy) = 0 – заменяем dy/y на дифференциал логарифма
d(y/x - ln Cy) = 0 – сумма дифференциалов = дифференциалу суммы
y/x - ln Cy = 0 – решение №1.

Проверкой убеждаемся, что x = 0 и y = 0 – также решения.
(0, 0) – особая точка уравнения, в ней решение не единственно.

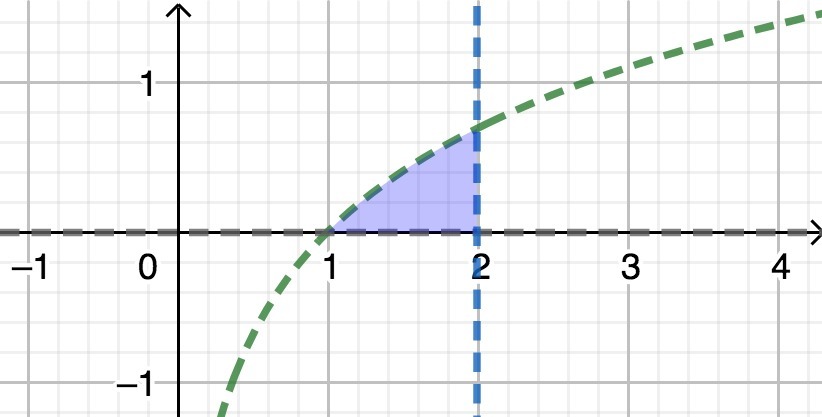
2) Область интегрирования изображена на рисунке. Двойной интеграл можно свести к повторным, для обоих порядков интегрирования получается не берущийся в элементарных функциях интеграл от exp(x)/x. Одна из его первообразных – интегральная экспонента Ei(x).

$displaystyleiint e^x,dx,dy=int_1^2e^x dxint_0^{ln x}dy=int_1^2e^xln x,dx=\=e^2ln2-int_1^2frac{e^x}x,dx=e^2ln2-Ei(2)+Ei(1)$
$displaystyleiint e^x,dx,dy=int_0^{ln 2}dyint_{e^y}^2e^x,dx=int_0^{ln2}(e^2-e^{e^y}),dy=\=e^2ln2-int_0^{ln2}e^{e^y},dy=left[begin{array}{c}x=e^y\y=ln x\dy=frac{dx}{x}end{array}right]=\=e^2ln2-int_1^2frac{e^x}{x},dx=e^2ln2-Ei(2)+Ei(1)$