Question

В равнобедренном треугольнике АВС с основанием АС отрезки AD и BH его высота. Найдите СD,если ВН=9 см sinA=0,6

Answer 1

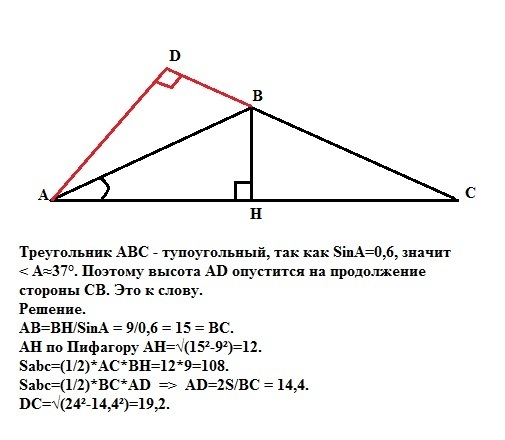
Треугольник АВС - тупоугольный, так как SinA=0,6, значит
< А≈37°. Поэтому высота АD опустится на продолжение стороны СВ. Это к слову.
Решение.
АВ=ВН/SinA = 9/0,6 = 15см = BC.
АН по Пифагору АН=√(15²-9²)=12см.
Sabc=(1/2)*AC*BH=12*9=108см².
Sabc=(1/2)*BC*AD  =>  AD=2S/BC = 14,4см.
DC=√(24²-14,4²)=19,2см.

Answer 2

спасибо)