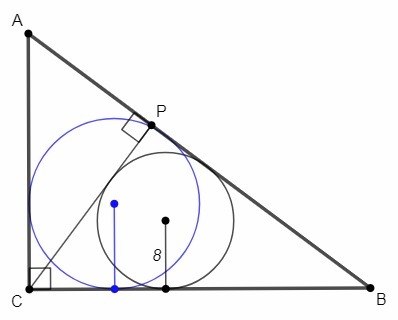
Из вершины прямого угла С треугольника АВС проведена высота СР. радиус окружности, вписанной в треугольник ВСР, равен 8, тангенс угла ВАС равен 4/3. найдите радиус вписанной окружности треугольника АВС.
Ответы
Ответ дал:
0
tg(BAC)=BC/AC =4/3
△ABC - египетский треугольник (стороны относятся как 3:4:5)
Высота из прямого угла делит треугольник на подобные друг другу и исходному.
△ABC~△BCP , AB/BC=5/4
Отношение соответствующих элементов подобных треугольников равно коэффициенту подобия.
R_abc/R_bcp =AB/BC => R_abc= 8*5/4 =10
Приложения:
Вас заинтересует
2 года назад
2 года назад
9 лет назад