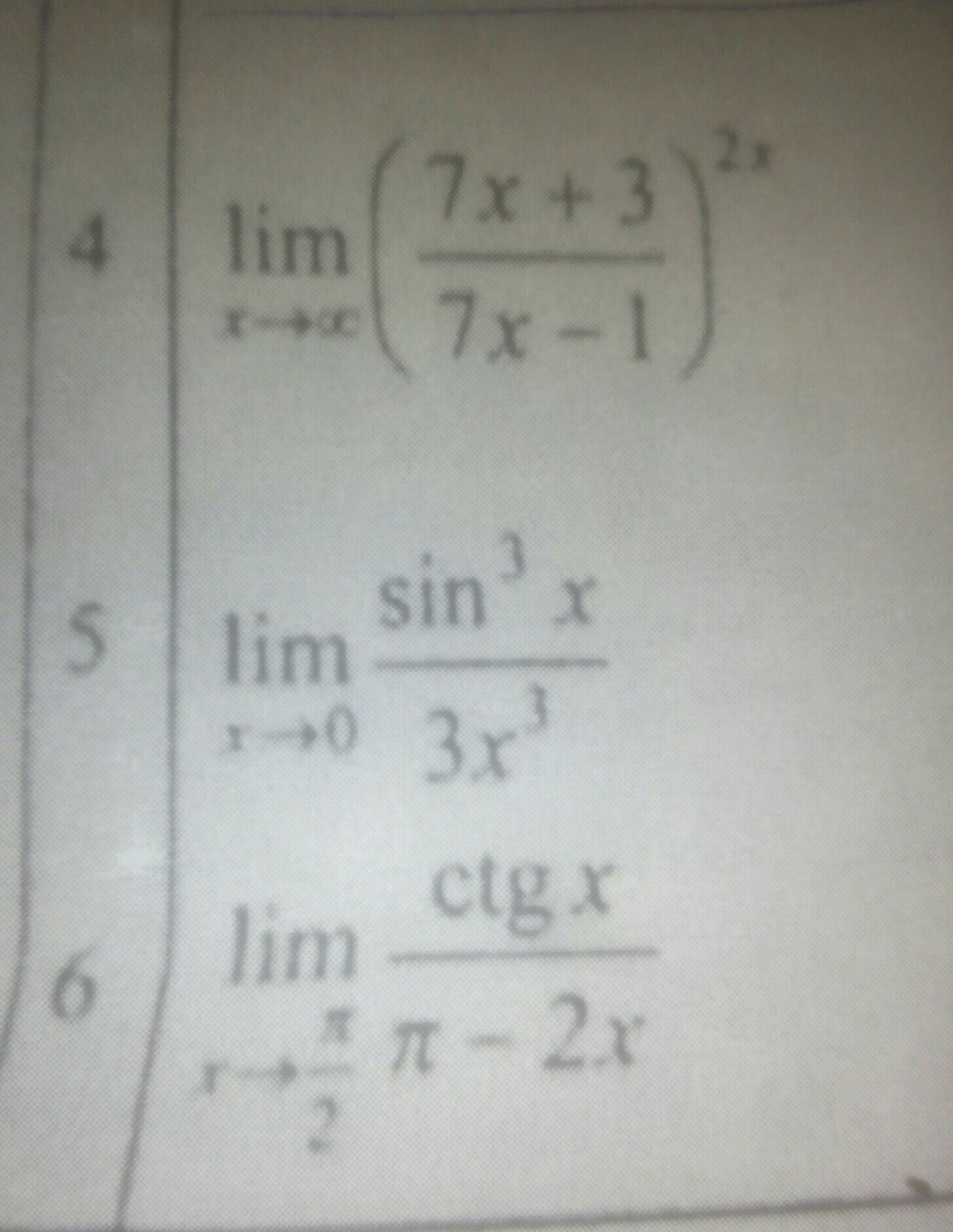Ответы
Ответ дал:
0
4)

Так как

То

Тогда:

5)

По первому замечательному пределу:

Тогда получаем:

6)

При подстановке значения x в выражение получаем неопределенность .
.
Сделаем замену:

Тогда:

Выполним преобразования:


Так как
То
Тогда:
5)
По первому замечательному пределу:
Тогда получаем:
6)
При подстановке значения x в выражение получаем неопределенность
Сделаем замену:
Тогда:
Выполним преобразования:
Вас заинтересует
2 года назад
3 года назад
9 лет назад
9 лет назад
10 лет назад