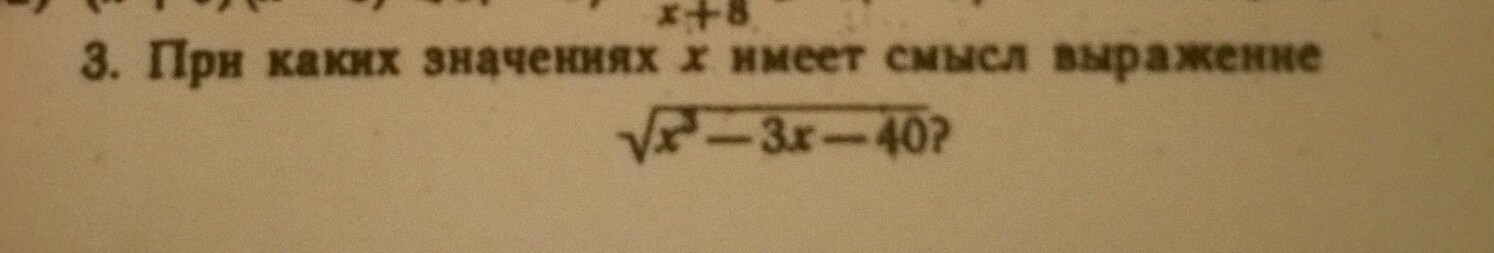Ответы
Ответ дал:
0
при условии неотрицательности подкоренного выражения:

Найдем точки пересечения оси OX графиком функции :
:

Пусть - корень уравнения (*)
- корень уравнения (*)
и представим его в виде: , где
, где  и
и пока что неизвестны, тогда:
пока что неизвестны, тогда:

----------------------
Пробуем наложить на и
и дополнительные условия:
дополнительные условия:

Получаем в этом случае, систему ур-й для и
и  :
:

По т. Виета, для любого такие
такие  и
и  действительно существуют, могут быть комплексными, и являються корнями ур-я:
действительно существуют, могут быть комплексными, и являються корнями ур-я:

Т.е. получилось наложить дополнительные ограничения на и
и  !!!
!!!
----------------
Если взять такие и
и  , досих пор неизвестные, то ур-е (**) сведётся к:
, досих пор неизвестные, то ур-е (**) сведётся к:

И тогда, возведя обе части ур-я в куб, и объединяя с ур-ем (***) получаем:
в куб, и объединяя с ур-ем (***) получаем:

Откуда за т. Виета и
и  являються корнями ур-я:
являються корнями ур-я:

тогда![x_{1,2,3}=a+b=sqrt[3]{20+sqrt{399}}+sqrt[3]{20-sqrt{399}} x_{1,2,3}=a+b=sqrt[3]{20+sqrt{399}}+sqrt[3]{20-sqrt{399}}](https://tex.z-dn.net/?f=x_%7B1%2C2%2C3%7D%3Da%2Bb%3Dsqrt%5B3%5D%7B20%2Bsqrt%7B399%7D%7D%2Bsqrt%5B3%5D%7B20-sqrt%7B399%7D%7D) - у каждого из этих кубических корней есть три значения, и только одно из них действительное, два других - коплекстны, что важно, для каждого выбранного значения первого кубического корня нужно выбирать соответсвующие значение второго кубического корня, что бы выполнялось условие:
- у каждого из этих кубических корней есть три значения, и только одно из них действительное, два других - коплекстны, что важно, для каждого выбранного значения первого кубического корня нужно выбирать соответсвующие значение второго кубического корня, что бы выполнялось условие: 
Теперь пробуем разложить на множители выражение:
пусть![A=sqrt[3]{20+sqrt{399}} A=sqrt[3]{20+sqrt{399}}](https://tex.z-dn.net/?f=A%3Dsqrt%5B3%5D%7B20%2Bsqrt%7B399%7D%7D) и
и ![B=sqrt[3]{20-sqrt{399}} B=sqrt[3]{20-sqrt{399}}](https://tex.z-dn.net/?f=B%3Dsqrt%5B3%5D%7B20-sqrt%7B399%7D%7D) (берем действительные значения сейчас и потом)
(берем действительные значения сейчас и потом)
замечаем, что

![A*B=sqrt[3]{20+sqrt{399}}*sqrt[3]{20-sqrt{399}}=\\
=sqrt[3]{(20+sqrt{399})*(20-sqrt{399})}=sqrt[3]{20^2-399}=sqrt[3]{1}=1 A*B=sqrt[3]{20+sqrt{399}}*sqrt[3]{20-sqrt{399}}=\\
=sqrt[3]{(20+sqrt{399})*(20-sqrt{399})}=sqrt[3]{20^2-399}=sqrt[3]{1}=1](https://tex.z-dn.net/?f=A%2AB%3Dsqrt%5B3%5D%7B20%2Bsqrt%7B399%7D%7D%2Asqrt%5B3%5D%7B20-sqrt%7B399%7D%7D%3D%5C%5C%0A%3Dsqrt%5B3%5D%7B%2820%2Bsqrt%7B399%7D%29%2A%2820-sqrt%7B399%7D%29%7D%3Dsqrt%5B3%5D%7B20%5E2-399%7D%3Dsqrt%5B3%5D%7B1%7D%3D1)
тогда:

![x^3+(A+B)x^2-3ABx-(A+B)x^2-\ -(A+B)(A^2+B^2-AB)=0\\ x^3+(A+B)x^2+(A^2+B^2-AB)x-(A+B)x^2-\-(A^2+2AB+B^2)x -(A+B)(A^2+B^2-AB)=0\\ x^3+(A+B)x^2+(A^2+B^2-AB)x-(A+B)x^2-(A+B)^2x-\ -(A+B)(A^2+B^2-AB)=0\\ x*[x^2+(A+B)x+(A^2+B^2-AB)]-\ -(A+B)*[x^2+(A+B)x+(A^2+B^2-AB)]=0\\ (x^2+(A+B)x+A^2+B^2-AB)*(x-(A+B))=0 x^3+(A+B)x^2-3ABx-(A+B)x^2-\ -(A+B)(A^2+B^2-AB)=0\\ x^3+(A+B)x^2+(A^2+B^2-AB)x-(A+B)x^2-\-(A^2+2AB+B^2)x -(A+B)(A^2+B^2-AB)=0\\ x^3+(A+B)x^2+(A^2+B^2-AB)x-(A+B)x^2-(A+B)^2x-\ -(A+B)(A^2+B^2-AB)=0\\ x*[x^2+(A+B)x+(A^2+B^2-AB)]-\ -(A+B)*[x^2+(A+B)x+(A^2+B^2-AB)]=0\\ (x^2+(A+B)x+A^2+B^2-AB)*(x-(A+B))=0](https://tex.z-dn.net/?f=x%5E3%2B%28A%2BB%29x%5E2-3ABx-%28A%2BB%29x%5E2-%5C+-%28A%2BB%29%28A%5E2%2BB%5E2-AB%29%3D0%5C%5C+x%5E3%2B%28A%2BB%29x%5E2%2B%28A%5E2%2BB%5E2-AB%29x-%28A%2BB%29x%5E2-%5C-%28A%5E2%2B2AB%2BB%5E2%29x+-%28A%2BB%29%28A%5E2%2BB%5E2-AB%29%3D0%5C%5C+x%5E3%2B%28A%2BB%29x%5E2%2B%28A%5E2%2BB%5E2-AB%29x-%28A%2BB%29x%5E2-%28A%2BB%29%5E2x-%5C+-%28A%2BB%29%28A%5E2%2BB%5E2-AB%29%3D0%5C%5C+x%2A%5Bx%5E2%2B%28A%2BB%29x%2B%28A%5E2%2BB%5E2-AB%29%5D-%5C+-%28A%2BB%29%2A%5Bx%5E2%2B%28A%2BB%29x%2B%28A%5E2%2BB%5E2-AB%29%5D%3D0%5C%5C+%28x%5E2%2B%28A%2BB%29x%2BA%5E2%2BB%5E2-AB%29%2A%28x-%28A%2BB%29%29%3D0)
Итак! Оценим дискриминант полученного квадратного трехчлена, а именно:


По скольку , то дискриминант отрицателен, т.е. квадратный трехчлен
, то дискриминант отрицателен, т.е. квадратный трехчлен  принимает исключительно положительные значения, и тогда, выражение
принимает исключительно положительные значения, и тогда, выражение  принимет неотрицательные значения лишь в случае когда
принимет неотрицательные значения лишь в случае когда
![x-(A+B) geq 0\\
x geq A+B\\
x geq sqrt[3]{20+sqrt{399}}+sqrt[3]{20-sqrt{399}}\\
xin[sqrt[3]{20+sqrt{399}}+sqrt[3]{20-sqrt{399}}; +infty) x-(A+B) geq 0\\
x geq A+B\\
x geq sqrt[3]{20+sqrt{399}}+sqrt[3]{20-sqrt{399}}\\
xin[sqrt[3]{20+sqrt{399}}+sqrt[3]{20-sqrt{399}}; +infty)](https://tex.z-dn.net/?f=x-%28A%2BB%29+geq+0%5C%5C%0Ax+geq+A%2BB%5C%5C%0Ax+geq+sqrt%5B3%5D%7B20%2Bsqrt%7B399%7D%7D%2Bsqrt%5B3%5D%7B20-sqrt%7B399%7D%7D%5C%5C%0Axin%5Bsqrt%5B3%5D%7B20%2Bsqrt%7B399%7D%7D%2Bsqrt%5B3%5D%7B20-sqrt%7B399%7D%7D%3B+%2Binfty%29)
Ответ:![[sqrt[3]{20+sqrt{399}}+sqrt[3]{20-sqrt{399}}; +infty) [sqrt[3]{20+sqrt{399}}+sqrt[3]{20-sqrt{399}}; +infty)](https://tex.z-dn.net/?f=%5Bsqrt%5B3%5D%7B20%2Bsqrt%7B399%7D%7D%2Bsqrt%5B3%5D%7B20-sqrt%7B399%7D%7D%3B+%2Binfty%29)
------------------------------------------
И в условии, пожалуй, опечатка, вместо куба, пожалуй, иммелся в виду квадрат!
при условии неотрицательности подкоренного выражения:
![x^2-3x-40 geq 0\\
D=(-3)^2-4*1*(-40)=9+160=169=13^2\\
x_{1,2}=frac{-(-3)pmsqrt{13^2}}{2*1}=frac{3pm13}{2}\\
x_1=8 x_2=-5\\
(x-8)(x-(-5)) geq 0\\
++++++[-5]--------[8]+++++++ textgreater x\\
xin(-infty; -5]cup[8; +infty) x^2-3x-40 geq 0\\
D=(-3)^2-4*1*(-40)=9+160=169=13^2\\
x_{1,2}=frac{-(-3)pmsqrt{13^2}}{2*1}=frac{3pm13}{2}\\
x_1=8 x_2=-5\\
(x-8)(x-(-5)) geq 0\\
++++++[-5]--------[8]+++++++ textgreater x\\
xin(-infty; -5]cup[8; +infty)](https://tex.z-dn.net/?f=x%5E2-3x-40+geq+0%5C%5C%0AD%3D%28-3%29%5E2-4%2A1%2A%28-40%29%3D9%2B160%3D169%3D13%5E2%5C%5C%0Ax_%7B1%2C2%7D%3Dfrac%7B-%28-3%29pmsqrt%7B13%5E2%7D%7D%7B2%2A1%7D%3Dfrac%7B3pm13%7D%7B2%7D%5C%5C%0Ax_1%3D8+++x_2%3D-5%5C%5C%0A%28x-8%29%28x-%28-5%29%29+geq+0%5C%5C%0A%2B%2B%2B%2B%2B%2B%5B-5%5D--------%5B8%5D%2B%2B%2B%2B%2B%2B%2B+textgreater++x%5C%5C%0Axin%28-infty%3B+-5%5Dcup%5B8%3B+%2Binfty%29)
Ответ:![(-infty; -5]cup[8; +infty) (-infty; -5]cup[8; +infty)](https://tex.z-dn.net/?f=%28-infty%3B+-5%5Dcup%5B8%3B+%2Binfty%29)
 ,
,
где и
и 
решения уравнения
Найдем точки пересечения оси OX графиком функции
Пусть
и представим его в виде:
----------------------
Пробуем наложить на
Получаем в этом случае, систему ур-й для
По т. Виета, для любого
Т.е. получилось наложить дополнительные ограничения на
----------------
Если взять такие
И тогда, возведя обе части ур-я
Откуда за т. Виета
тогда
Теперь пробуем разложить на множители выражение:
пусть
замечаем, что
тогда:
Итак! Оценим дискриминант полученного квадратного трехчлена, а именно:
По скольку
Ответ:
------------------------------------------
И в условии, пожалуй, опечатка, вместо куба, пожалуй, иммелся в виду квадрат!
при условии неотрицательности подкоренного выражения:
Ответ:
где
решения уравнения
Ответ дал:
0
вместо "и тогда, выражение x^3-3x-40 принимет положительные лишь " должно быть: "и тогда, выражение x^3-3x-40 принимет НЕОТРИЦАТЕЛЬНЫЕ лишь
Вас заинтересует
2 года назад
3 года назад
10 лет назад
10 лет назад