Ответы
Ответ дал:
0
C1.
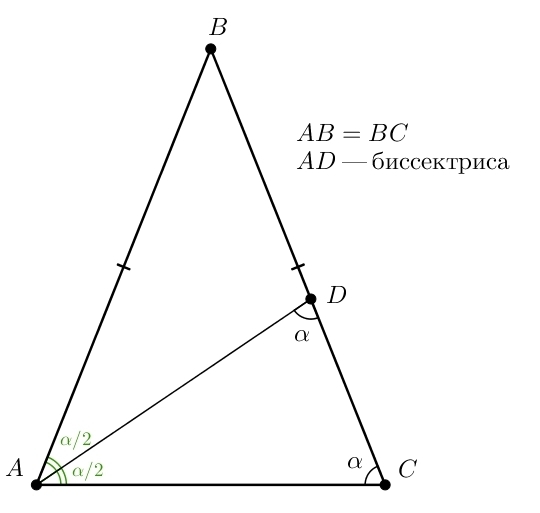
Обозначим угол при основании как (см. рисунок). Сумма углов любого треугольника равна 180°. Поэтому для треугольника ADC имеем:
(см. рисунок). Сумма углов любого треугольника равна 180°. Поэтому для треугольника ADC имеем:
 .
.
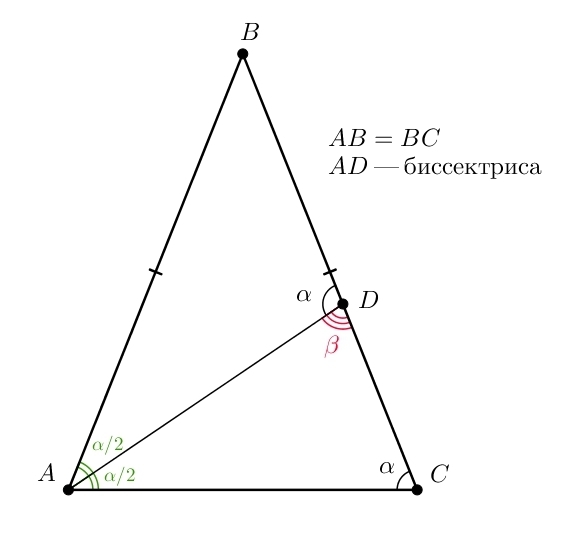
Для полноты решения нужно рассмотреть ещё один случай. Фраза «пересекает под углом» может означать, что — это угол ∠BDA (см. рисунок 2). Тогда по теореме о смежных углах их сумма равна 180°, то есть угол β равен 180°–α. Тогда имеем:
— это угол ∠BDA (см. рисунок 2). Тогда по теореме о смежных углах их сумма равна 180°, то есть угол β равен 180°–α. Тогда имеем:

Этим доказано, что такой треугольник невозможен.
Ответ: 72°.
С2
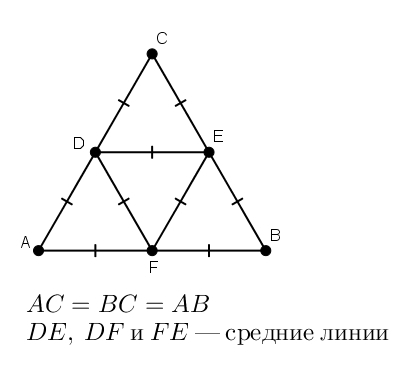
Судя по всему, на 4 треугольника. Чтобы это сделать, надо провести три средние линии (отрезки, соединяющие середины двух сторон треугольника; см. рисунок 3). По теореме средняя линия равна половина стороны (и параллельна ей). Поэтому все 4 треугольника — равносторонние.
Обозначим угол при основании как
Для полноты решения нужно рассмотреть ещё один случай. Фраза «пересекает под углом» может означать, что
Этим доказано, что такой треугольник невозможен.
Ответ: 72°.
С2
Судя по всему, на 4 треугольника. Чтобы это сделать, надо провести три средние линии (отрезки, соединяющие середины двух сторон треугольника; см. рисунок 3). По теореме средняя линия равна половина стороны (и параллельна ей). Поэтому все 4 треугольника — равносторонние.
Приложения:
Вас заинтересует
2 года назад
3 года назад
3 года назад
9 лет назад
9 лет назад
10 лет назад
