Question

Какие из углов, изображённых на картинке, равны?

Answer 1

Ответ:

A,B,D,E

Пошаговое объяснение:

Answer 2

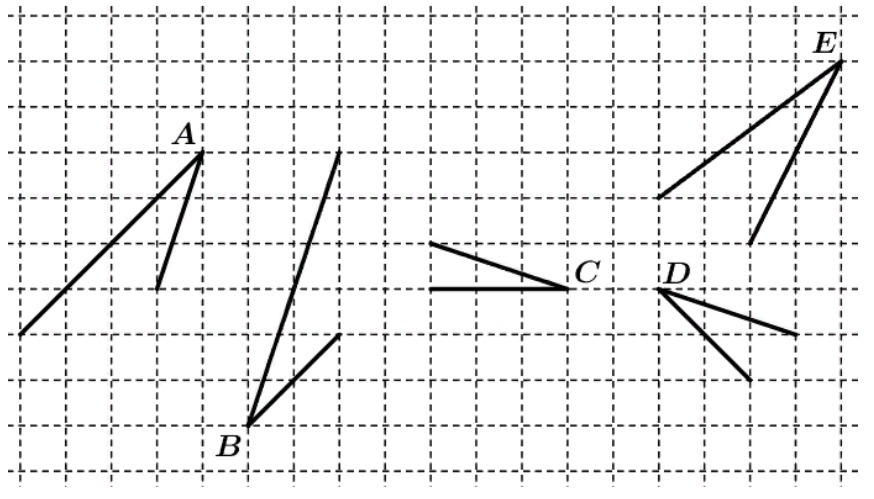
По внешнему виду определить, какие из углов равны, невозможно, если градусные меры углов близки по своим значениям. Нужно вычислять. Можно разными способами.  Например, через скалярное произведение векторов можно найти косинусы углов и сравнить их.

$vec acdot vec b=|vec a|cdot |vec b|cdot cos hat{(vec a; vec b)}$

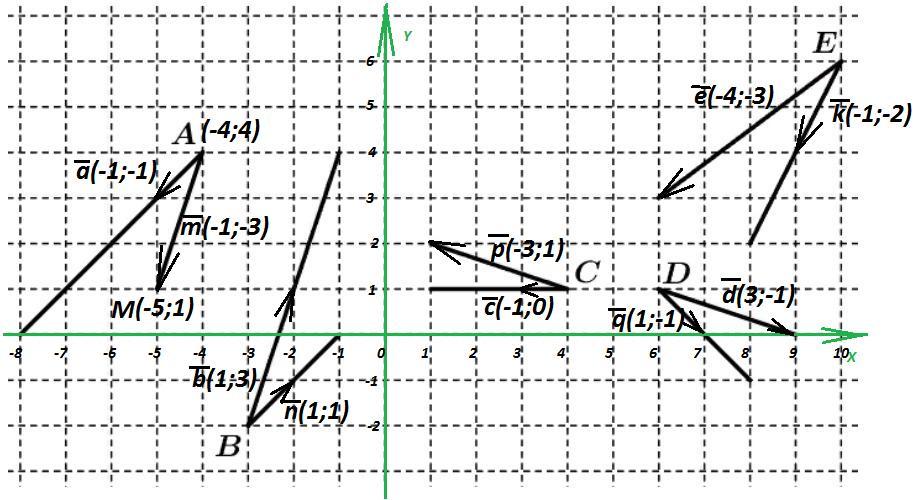
Произвольно построим прямоугольную систему координат XOY. Каждый изображённый угол образуют два вектора. Их координаты легко определить по узлам сетки. Например, координаты вектора $vec m=vec {MA}=(x_M-x_A;y_M-y_A)=(-5-(-4);1-4)=(-1;-3)$

1. ∠A;   $vec a(-1;-1);~~~vec m(-1; -3)$

$boldsymbol{cos angle A=}cos hat{(vec a;vec m)}=dfrac {-1cdot (-1)-1cdot (-3)}{sqrt{(-1)^2+(-1)^2}sqrt{(-1)^2+(-3)^2}}=boldsymbol{dfrac 2{sqrt5}}$

2. ∠B;   $vec b(1;3);~~~vec n(1; 1)$

$boldsymbol{cos angle B=}cos hat{(vec b;vec n)}=dfrac {1cdot 1+3cdot 1}{sqrt{1^2+3^2}sqrt{1^2+1^2}}=dfrac{4}{sqrt{10}sqrt{2}}=boldsymbol{dfrac 2{sqrt5}}$

3. ∠C;   $vec c(-1;0);~~~vec p(-3; 1)$

$boldsymbol{cos angle C=}cos hat{(vec c;vec p)}=dfrac {-1cdot (-3)+0cdot 1}{sqrt{(-1)^2+0^2}sqrt{(-3)^2+1^2}}=boldsymbol{dfrac 3{sqrt{10}}}$

4. ∠D;   $vec d(3;-1);~~~vec q(1; -1)$

$boldsymbol{cos angle D=}cos hat{(vec d;vec q)}=dfrac {3cdot 1-1cdot (-1)}{sqrt{3^2+(-1)^2}sqrt{1^2+(-1)^2}}=boldsymbol{dfrac 2{sqrt5}}$

5. ∠E;   $vec e(-4;-3);~~~vec k(-1; -2)$

$boldsymbol{cos angle E=}cos hat{(vec e;vec k)}=dfrac {-4cdot (-1)-3cdot (-2)}{sqrt{(-4)^2+(-3)^2}sqrt{(-1)^2+(-2)^2}}=boldsymbol{dfrac 2{sqrt5}}$

cos ∠A = cos ∠B = cos ∠D = cos ∠E =$boldsymbol{dfrac 2{sqrt5}}$

Ответ: ∠A = ∠B = ∠D = ∠E