Question

Помогите пожалуйста. Хорда AD окружности пересекает два взаимо перпендикулярных радиуса этой окружности в точках B и C, причём точка B лежит между точками A и C. Известно, что AB:BC:CD=3:4:5, а радиус окружности равен 3√13. Найдите длину хорды AD.

Answer 1

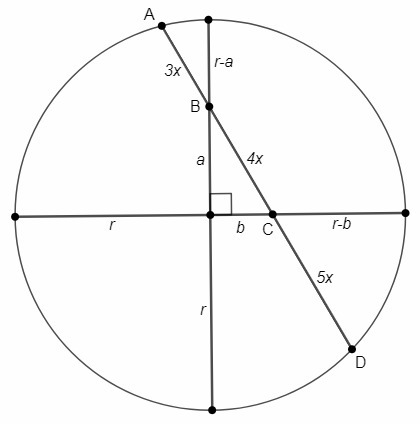
Если две хорды пересекаются, то произведение отрезков одной хорды равно произведению отрезков другой хорды.

3x * 9x = (r-a)(r+a) 
5x * 7x = (r-b)(r+b)

16x^2 = a^2 +b^2 (по т. Пифагора)

27x^2 = r^2 - a^2
35x^2 = r^2 - b^2
----------------------------
62x^2 = 2r^2 -(a^2 +b^2) <=>
62x^2 = 2r^2 -16x^2 <=>
78x^2 = 2r^2 <=> 
x = r/√39 = 3√13/√39 = √3

AD= 12x =12√3

Answer 2

первые 2 строчки надо бы описать подробнее...

Answer 3

теперь вижу, спасибо!