Question

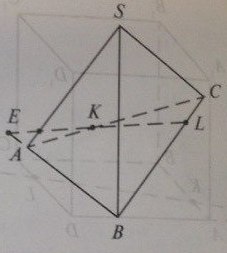
В пирамиде SABC все ребра равны a. На ребре АС выбрана точка К, на ребре ВС - точка L. При этом АК:КС=1:2, СL:LB=1:4. Через точки К, L, S проведена плоскость. Используя рисунок, ответьте: какова длина отрезка АЕ и LE?

Answer 1

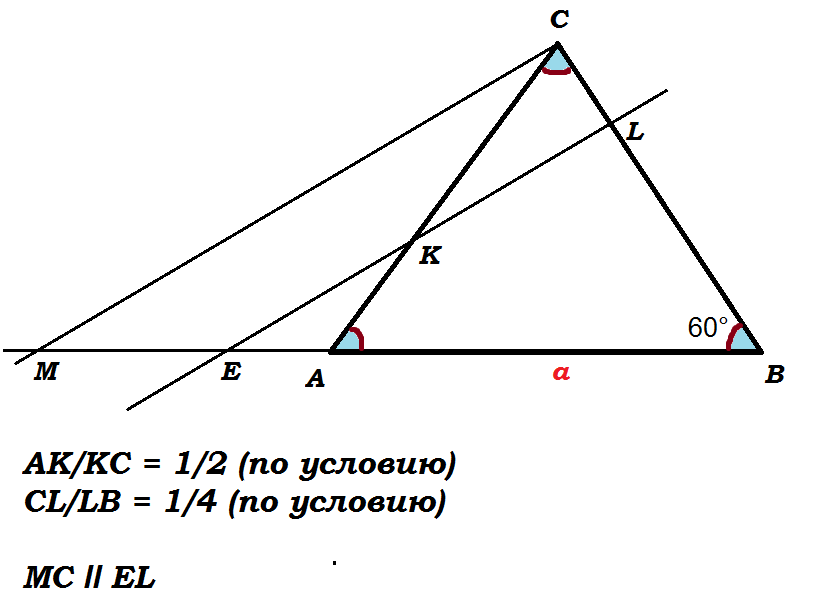
АС = СВ = ВА = а ( по условию) ==> ∆АВС - равносторонний 
проведем через пункт С прямую, параллельную прямой EL, пункт пересечения этой прямой с прямой АВ обозначим М
СМ ll EL
по т. Фалеса имеем 
ME/EB =  CL/LB = 1/4 = 2/8
также по т. Фалеса:
ME/EA = CK/KA = 2/1

раз МЕ/ЕВ = 2/8
а МЕ/ЕА = 2/1, то ЕВ/ЕА = 8/1, то есть ЕА составляет 1/7 часть от АВ
EA = AB/7 = a/7
CL/LB = 1/4, значит LB составляет 4/5 от СВ  
LB = 4CB/5 = 4a/5

теперь найдем EL по т. косинусов :
<ABL = 60° (∆ABC - равносторонний)
EB = EA + AB = a/7 + a = 8a/7
LB = 4a/5
EL^2 = EB^2 + LB^2 - 2*EB* LB cos (<ABL) 
EL^2 = 64a^2/49 + 16a^2/25 - 2* 8a/7 * 4a/5  * 1/2
EL^2 = 64a^2/49 + 16a^2/25 - 32a^2/35
EL^2 = 1600a^2/1225 + 784a^2/1225 - 1120a^2/1225
EL^2 = (1600a^2 + 784a^2 - 1120a^2)/1225
EL^2 = 1264a^2/1225
EL = √(1264a^2/1225) = 4a(√79)/35

Answer 2

??

Answer 3

раз МЕ/ЕВ = 2/8, а МЕ/ЕА = 2/1, то ЕВ/ЕА не равно 1/8. EB больше EA. В 8 раз.