помогите пожалуйста. болела и пропустила тему. Докажите что при любых допустимых значениях переменных целым числом является значение выражения:
Приложения:
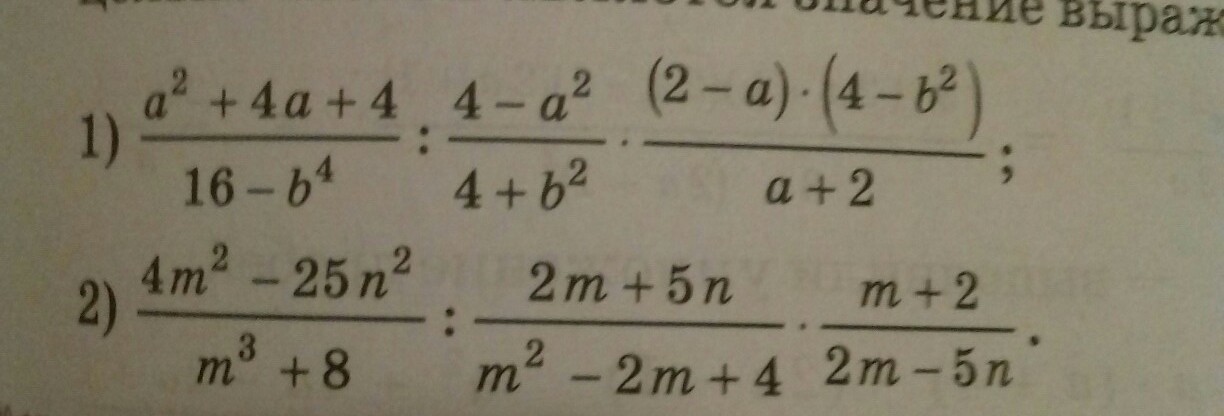
Ответы
Ответ дал:
0
1)

Значение выражения не зависит от значения переменных а,b
и равно 1. ⇒ 1∈ Z ( Z - множество целых чисел)
2)

1∈ Z , что и требовалось доказать.
Значение выражения не зависит от значения переменных а,b
и равно 1. ⇒ 1∈ Z ( Z - множество целых чисел)
2)
1∈ Z , что и требовалось доказать.
Вас заинтересует
2 года назад
2 года назад
3 года назад
3 года назад
9 лет назад
9 лет назад
10 лет назад