Question

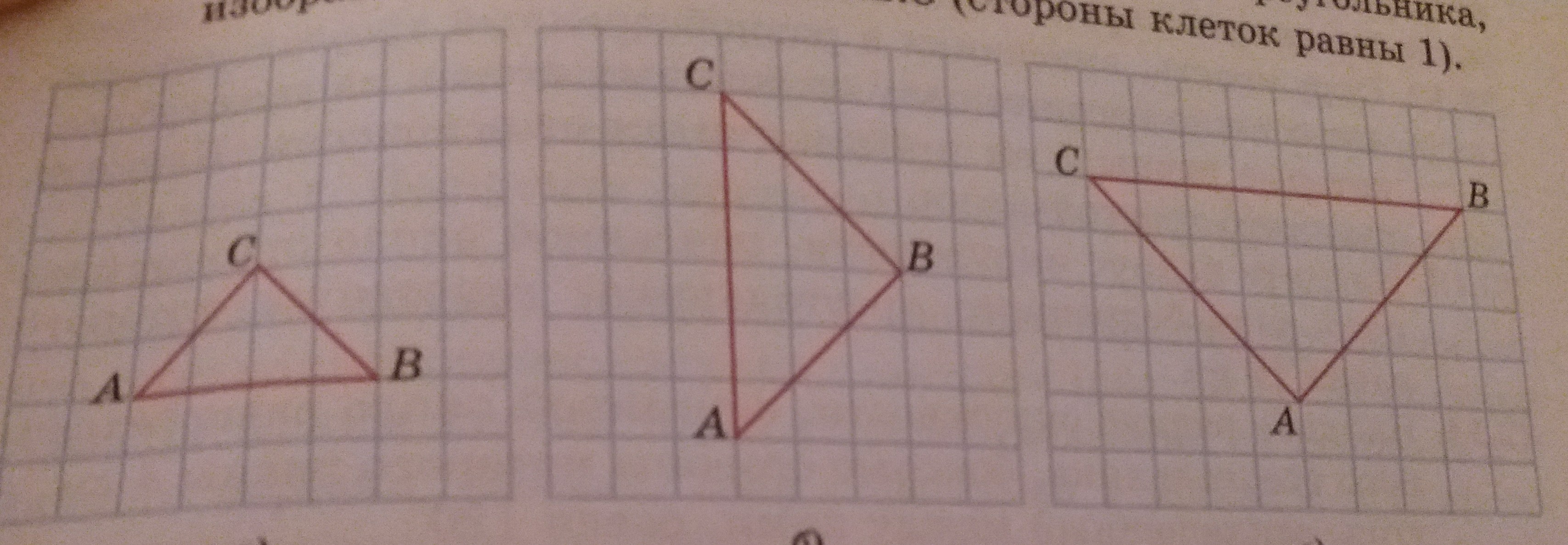
найдите радиус окружности, описанной около треугольника, изображенного на рисунке 22.8(стороны клеток равны 1)

Answer 1

Каждая тетрадная клетка - квадрат. Диагональ квадрата делит прямой угол пополам  ⇒  90°/2 = 45°.

Каждый из трёх треугольников равнобедренный прямоугольный, так как катеты образуют с гипотенузами углы 45°.  ⇒
Сумма углов треугольника:     45°+45°+90° = 180°
В прямоугольном треугольнике гипотенуза является диаметром описанной окружности. Чтобы найти радиус R, нужно посчитать длину гипотенузы по клеткам, а затем поделить её пополам.
---------------------------------------------------------
1) ΔABC:  ∠C = 90°; катеты AC = BC; гипотенуза AB = 4
  R = AB/2 = 4/2 = 2

2) ΔABC:  ∠B = 90°; катеты AB = BC; гипотенуза AC = 6
  R = AC/2 = 6/2 = 3

3) ΔABC:  ∠A = 90°; катеты AC = AB; гипотенуза BC = 8
  R = BC/2 = 8/2 = 4