Question

Решите неравенство (3x-8)²≥(8x-3)²
Срочно нужна помощь к завтрашнему дню!

Answer 1

9x^2+64-48x>=64x^2+9-48x
-55x^2>=- 55
x^2<=1
x<=(+-1)
Ответ: [-1;1]

Answer 2

Корни квадратного уравнения:x1=−1;x2=19x2−48x+64≥64x2−48x+9⇒9x2−48x+64≥64x2−48x+9⇒9x2−48x+64−64x2+48x−9≥0⇒9x2−48x+64−64x2+48x−9≥0⇒−55x2+55≥0−55x2+55≥0Решим квадратное уравнение −55x2+55=0
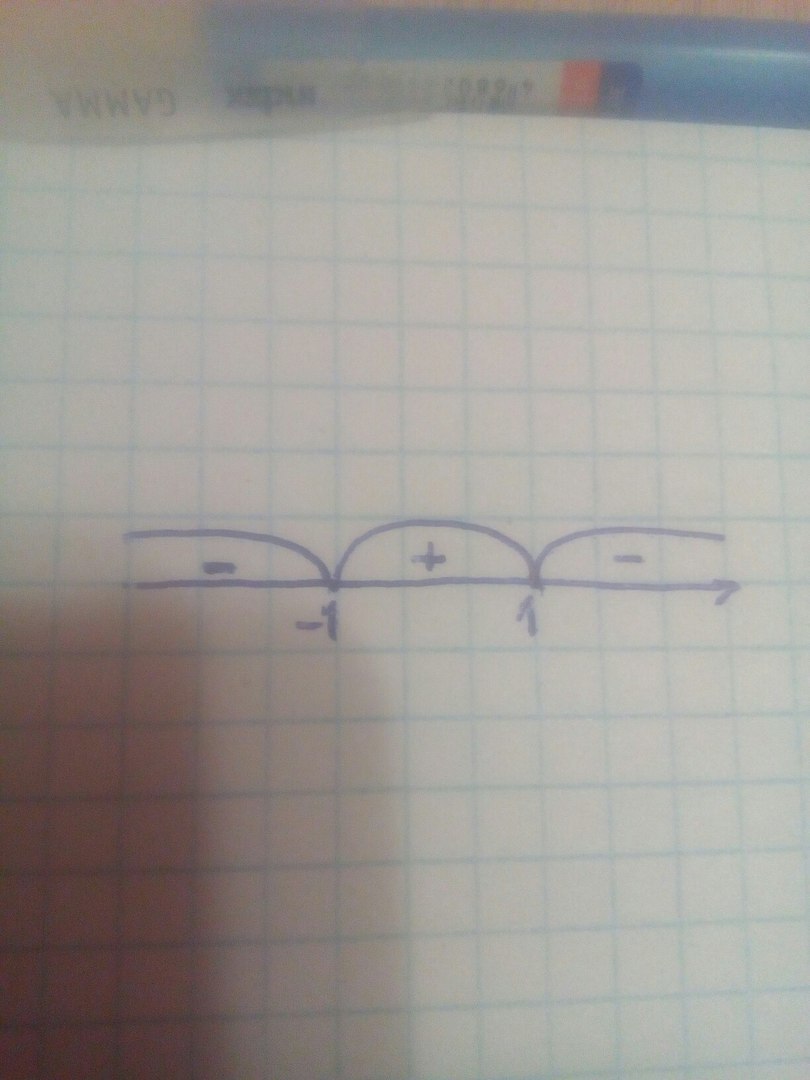
Наносим найденные точки на числовую ось и вычисляем знаки на каждом интервале:(как показано на изображении)
Ответ:x∈[−1;1]x∈[−1;1]или−1≤x≤1

Answer 3

(3x - 8)² ≥ (8x - 3)²

(3x - 8)² - (8x - 3)² ≥ 0

По формуле разности квадратов  a²-b²=(a-b)(a+b)

(3x - 8 - 8x + 3)(3x - 8 + 8x - 3) ≥ 0

(-5x - 5)(11x - 11) ≥ 0

Метод интервалов

-5x - 5 = 0;  x₁ = -1;       11x - 11 = 0;  x₂ = 1

-------------- [-1] +++++++++ [1] --------------> x

Ответ : x ∈ [-1; 1]