Question

РЕШИТЕ СРОЧНО ДАЮ 98 БАЛЛОВ!!!
№1
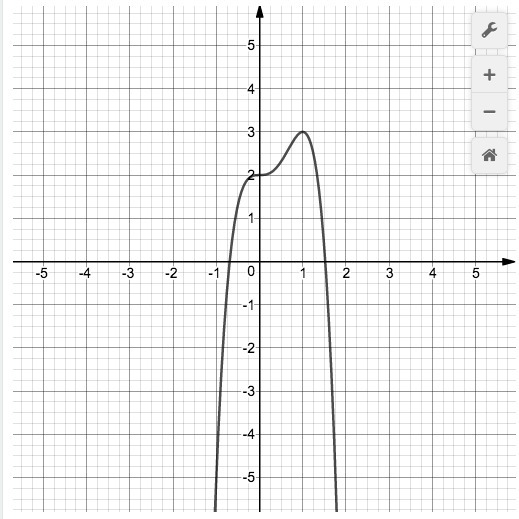
Найдите у наиб и у наим на интервале [0;+∞]
№2
Найдите наибольшее и наименьшее значения заданной функции на заданном интервале:
а)y=-x^2 - 6x + 1 на (-∞;-2]
б)y=x^3 - 3x^2 - 9x + 1 на [1;+∞)

Answer 1

1) yнаибольшее – ищем наибольшую точку на данном промежутке, т.е. выше которой графика нет на данном интервале,  и смотрим ее координату на оси y: это 3. 
yнаименьшее – на промежутке [1; +∞) функция убывает, то есть принимает все меньшие и меньшие значения с большим и большим x. Поэтому мы не можем найти наименьшее значение, ведь его точного нет: мы не можем увидеть конечную точку, а значения функции, как было сказано, уменьшаются с увеличением x, то есть до бесконечности. 

2) Экстремумы (а максимум/минимум функции – это и есть) ищутся так: вы находите производную и ищете ее нули. Смотрите промежутки возрастания/убывания функции (если удобно, можно сразу посмотреть значения нулей) и делаете выводы. 
В случае с отрезком нужно рассмотреть не только нули производной, но и значения функции на концах отрезка: например, если функция монотонно убывает и мы ищем максимум на отрезке, ясно, что он будет в левом конце отрезка. Теперь сделаем это для наших примеров. 


а) f'(x) = -2x - 6
Ищем нули производной: -2x - 6 = 0, x = -3. 
Функция возрастает, если значение производной больше нуля, и убывает, если меньше. Т.е. при x < -3 функция возрастает, при x > -3 – убывает. Значит, чем меньше x, тем меньше y – поэтому мы не можем найти минимум на данном отрезке, ведь при x → -∞ и y → -∞, поэтому мы не можем найти минимум. Рассматривать интервал [-3; -2] не имеет смысла: на нем y > 0 (будет меньше, когда пересечет нуль функции), а наши значения на минус бесконечности отрицательные (можем подтвердить это пределом $lim_{x to -infty} -x^2 - 6x + 1 = -infty$ или простыми размышлениями: функция пересечет другой нуль функции и, т.к. она убывает, значения там будут отрицательными. Можно еще посмотреть на график функции). 
Т.к. функция возрастает до x = -3, а после – убывает, x = -3 – максимум. Можно не проверять значения на концах отрезка, ведь больше нулей у производной нет, и это – вершина параболы ветвями вниз, которая и является максимумом функции. Значение максимума: y = 10. 

б) Поступим также: сначала найдем производную. 
f'(x) = 3x² - 6x - 9
Найдем нули: x² - 2x - 3 = 0, x = -1 и x = 3. 
До -1 возрастает, после до 3 – убывает, после 3 – возрастает. Значит, x = 3 может быть минимумом, а максимум мы опять не можем найти, ведь функция возрастает и значения могут быть бесконечно большими. 
На всякий случай проверим конец отрезка: x = 1, y = -10. Отобранный нуль производной: x = 3, y = -26. Это минимум на данном промежутке. Можно опять проверить по графику. 


Ответ: 1) yнаибольшее = 3, yнаименьшее – нет; 2) а) минимума нет, максимум – y = 10; б) максимума нет, минимум - y = -26. 
Задавайте вопросы в комментарии, если непонятно.