Ответы
Ответ дал:
0
У ромба противоположные углы равны. Значит ADC=ABC=54, a BCD=BAD=180-54=126.
AC - диагональ ромба и биссектриса, делит угол BCD пополам.
126:2= 63
Ответ: 63
AC - диагональ ромба и биссектриса, делит угол BCD пополам.
126:2= 63
Ответ: 63
Ответ дал:
0
Ответ:
63°
Пошаговое объяснение:
Выполним рисунок.
Вариант решения №1.
В ромбе противолежащие углы равны и сумма внутренних углов равна 360°. Диагонали ромба являются также и биссектрисами его углов.
Значит:
∠ACB=∠DCB/2=x°
∠ADC=∠ABC=54°
∠DAB=∠DCB=2x°
2*(∠ADC+∠DCB)=360° ⇒ 2(54+2x)=360 ⇒ 4x=360-108 ⇒ x = 63°.
Вариант решения №2.
В ромбе противолежащие углы равны и все стороны равны. Рассмотрим ΔАВС. Т.к. АВ=ВС, то он равнобедренный с углами при основании ∠САВ=∠АСВ=х. Тк. ∠ADC=∠ABC=54° и сумма внутренних углов треугольника равна 180°, то
Значит:
∠ACB+∠САВ+∠ABC=180°
2х+54=180 ⇒ 2х=126 ⇒ x = 63°.
Приложения:
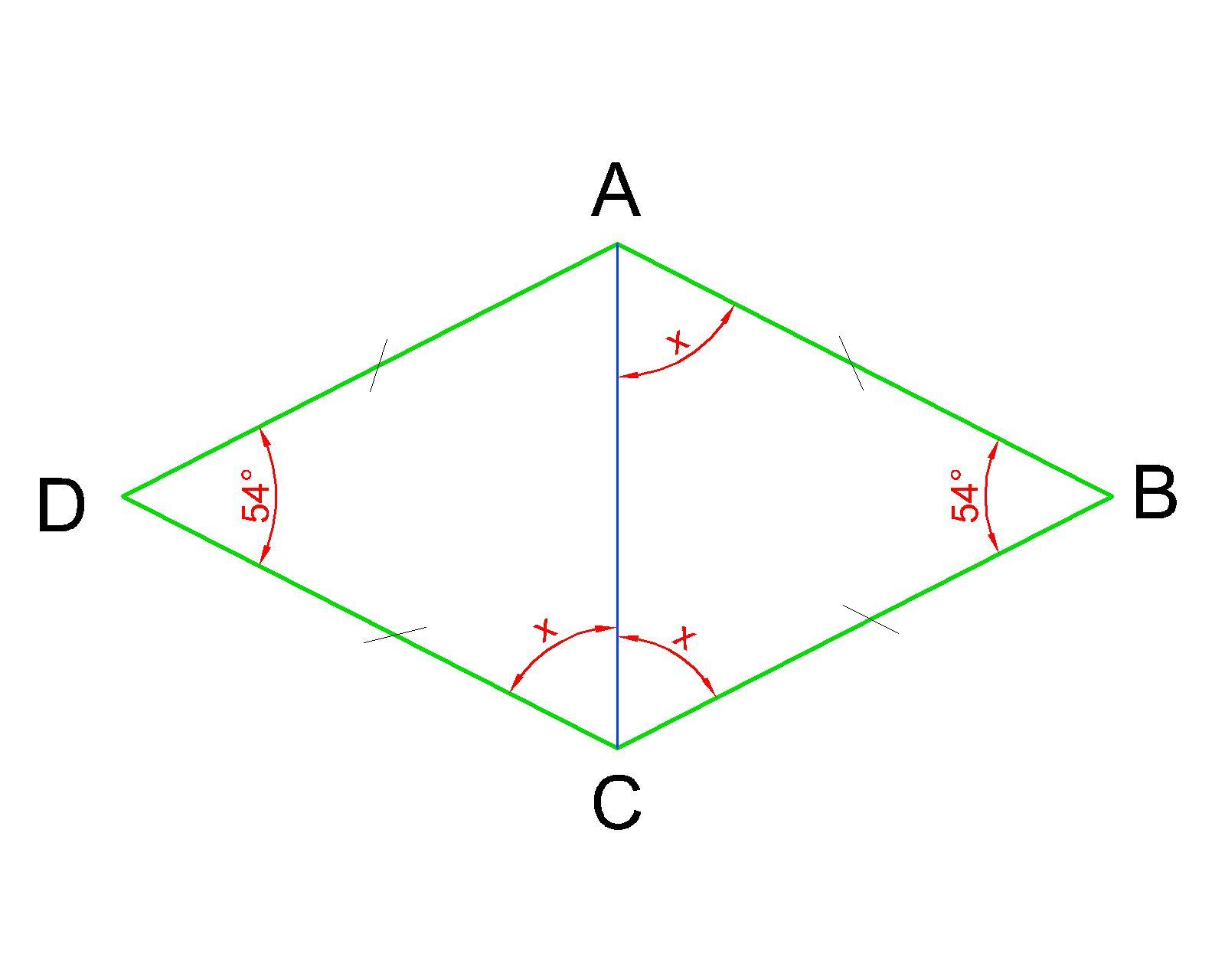
Вас заинтересует
2 года назад
3 года назад
9 лет назад
10 лет назад