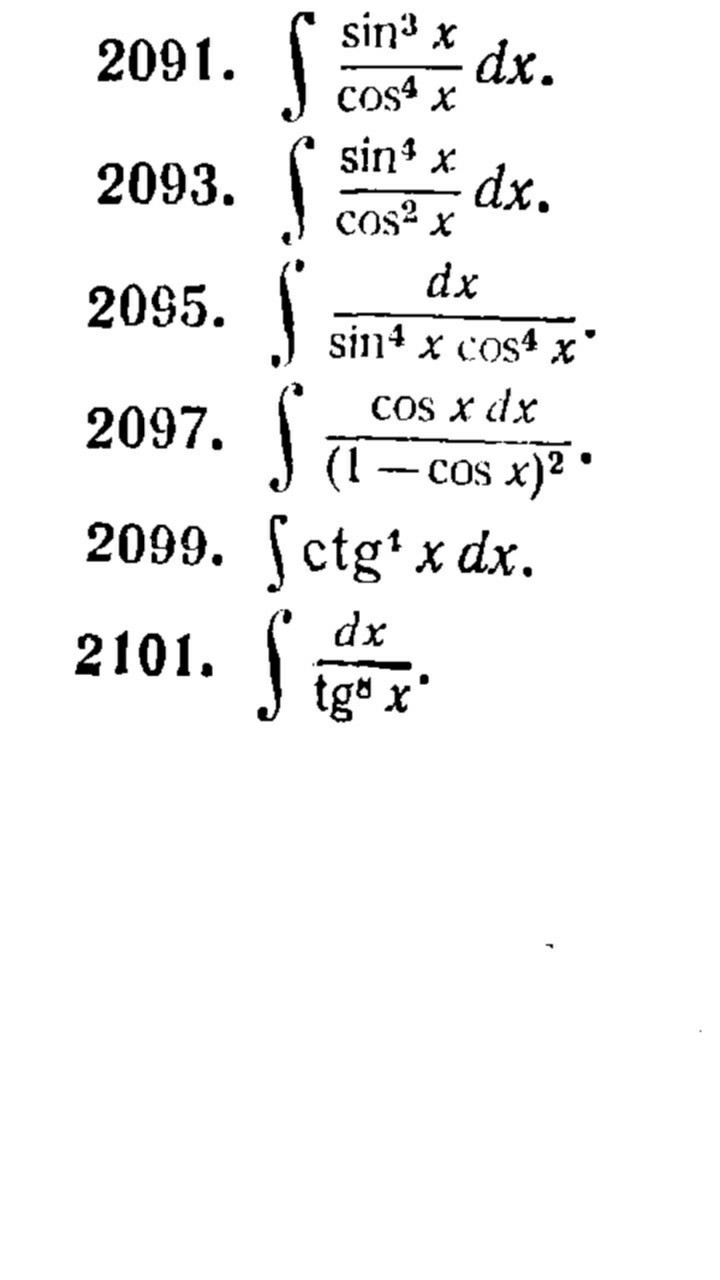Ответы
Ответ дал:
0
2095

Дальше простой рациональный интеграл
2099 - не видно степень котангенса
2101

Дальше простой рациональный интеграл
Дальше простой рациональный интеграл
2099 - не видно степень котангенса
2101
Дальше простой рациональный интеграл
Вас заинтересует
2 года назад
3 года назад
3 года назад
9 лет назад
9 лет назад
10 лет назад