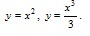Ответы
Ответ дал:
0
Находим абсциссы границ фигуры, приравнивая функции.
х² = х³/3,
(3х² - х³)/3 = 0.
Приравниваем нулю числитель:
3х² - х³ = 0,
х²(3 - х) = 0.
Получаем 2 точки: х = 0 и х = 3.

х² = х³/3,
(3х² - х³)/3 = 0.
Приравниваем нулю числитель:
3х² - х³ = 0,
х²(3 - х) = 0.
Получаем 2 точки: х = 0 и х = 3.
Вас заинтересует
2 года назад
3 года назад
3 года назад
9 лет назад
9 лет назад
10 лет назад