Ответы
Ответ дал:
0
Ответ дал:
0
x=±4 - стационарные точки
Ответ дал:
0
Я понял ,немного поспешил
Ответ дал:
0
Решение во вложении. Успехов в алгебре!
Приложения:
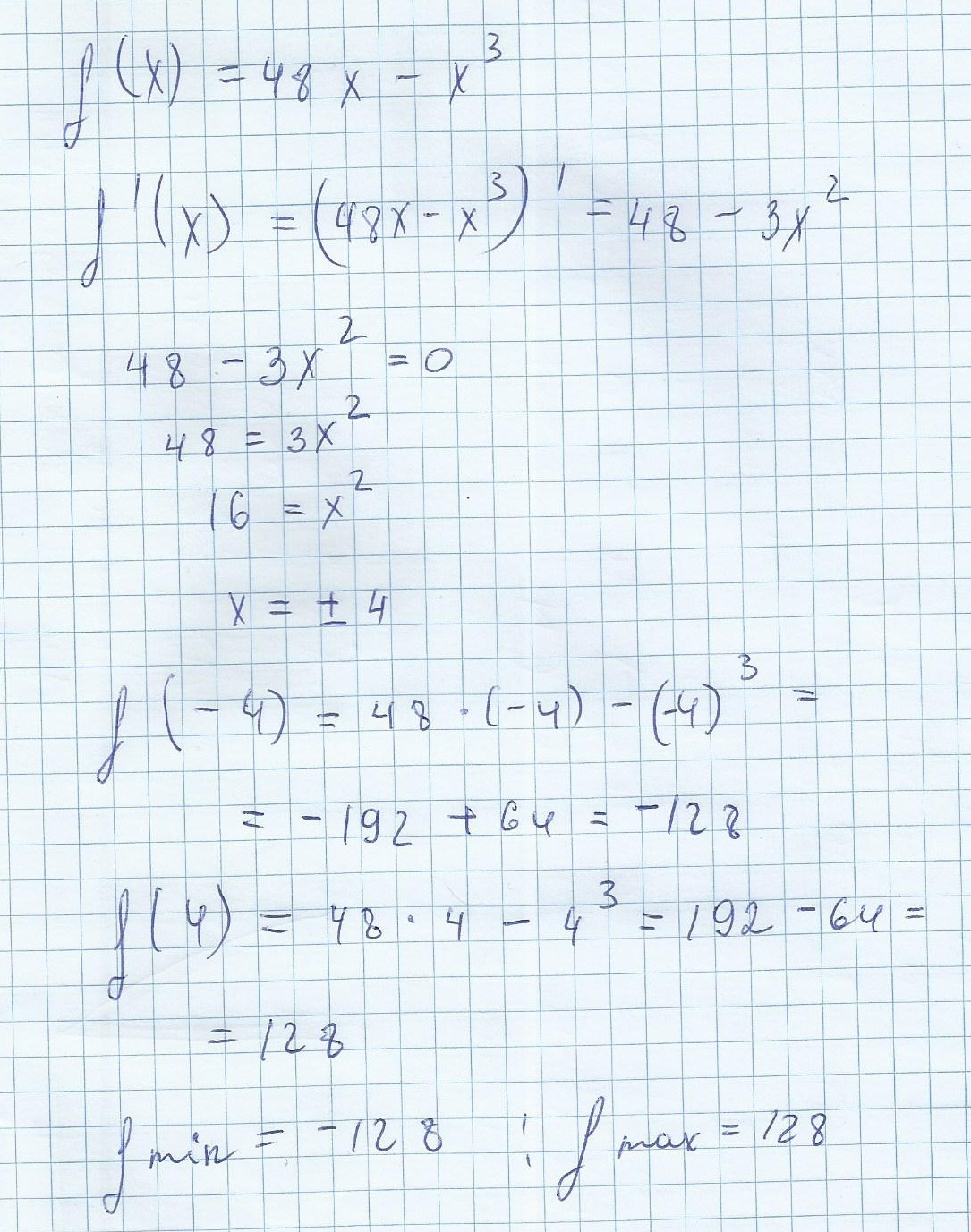
Вас заинтересует
2 года назад
3 года назад
3 года назад
9 лет назад