Question

ПОЖАЛУЙСТА, СРОЧНО!
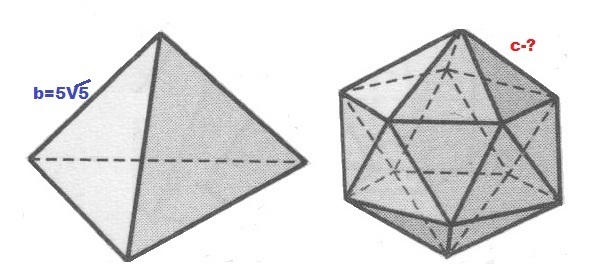
правильный тетраэдр и правильный икосаэдр имеют равную площадь полной поверхности ребро тетраэдра равно 5 корней из 5, тогда ребро икосаэдра равно..

Answer 1

Правильный тетраэдр - треугольная пирамида, все 4 грани которой равные равносторонние треугольники.
Правильный икосаэдр - двадцатигранник, все грани которого равные равносторонние треугольники.

Ребро тетраэдра - сторона равностороннего треугольника: b = 5√5
Площадь равностороннего треугольника
$S_1= frac{b^2 sqrt{3} }{4} = frac{(5 sqrt{5} )^2* sqrt{3} }{4} = frac{125 sqrt{3} }{4}$
Площадь полной поверхности правильного тетраэдра
$S_m=4* frac{125 sqrt{3} }{4} =125 sqrt{3}$

Площадь полной поверхности правильного тетраэдра и площадь полной поверхности правильного икосаэдра по условию равны.

Правильный икосаэдр имеет 20 граней. Площадь одной грани
$S_2= frac{S_m}{20} = frac{125 sqrt{3} }{20} = frac{25 sqrt{3} }{4}$
Площадь равностороннего треугольника со стороной c:
$S_2 = frac{c^2 sqrt{3} }{4} = frac{25 sqrt{3} }{4} \ \ c^2=25; c=5$

Ответ: ребро икосаэдра равно 5