Ответы
Ответ дал:
0
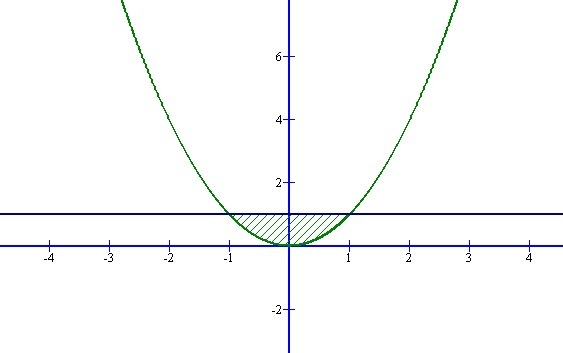
y = x² - парабола, ветви направлены вверх.
у=1 - прямая, параллельная оси абсцисс...
Если на отрезке![[a;b] [a;b]](https://tex.z-dn.net/?f=%5Ba%3Bb%5D) некоторая непрерывная функция
некоторая непрерывная функция  больше либо равна некоторой непрерывной функции
больше либо равна некоторой непрерывной функции  , то площадь фигуры, ограниченной графиками данных функций и прямыми
, то площадь фигуры, ограниченной графиками данных функций и прямыми  ,
,  , можно найти по формуле:
, можно найти по формуле:

Искомая площадь:
у=1 - прямая, параллельная оси абсцисс...
Если на отрезке
Искомая площадь:
Приложения:
Вас заинтересует
2 года назад
2 года назад
3 года назад
3 года назад
9 лет назад
10 лет назад