Задание 1.
Преобразуйте выражение, чтобы получить многочлен стандартного вида. Укажите степень многочлена.
Задание 2.
Докажите, что при любых целых значениях x многочлен делится на 7.
Задание 3.
Докажите, что при любых действительных значениях x многочлен не может принимать отрицательных значений.
Приложения:
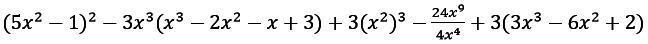
Ответы
Ответ дал:
0
Многочлен стандартного вида:

4-я степень.
Можно записать многочлен по-иному:

Очевидно, многочлен делится на 7, т.к. один из его множителей равен 7.
Пусть,


Мы видим, что у нас только один возможный корень (значение нас не интересует), значит, график лишь 1 раз коснется оси X; значит минимальное значение многочлена - ноль, т.е. нет отрицательных значений
4-я степень.
Можно записать многочлен по-иному:
Очевидно, многочлен делится на 7, т.к. один из его множителей равен 7.
Пусть,
Мы видим, что у нас только один возможный корень (значение нас не интересует), значит, график лишь 1 раз коснется оси X; значит минимальное значение многочлена - ноль, т.е. нет отрицательных значений
Ответ дал:
0
вы с интернет урока?
Ответ дал:
0
в каком смысле?
Ответ дал:
0
интернет урок - это что-то вроде спец. форума? Если вы о подобном, то нет; я обыкновенный ученик 9 класса
Ответ дал:
0
нет, интернет урок это домашняя школа)
Вас заинтересует
2 года назад
3 года назад
3 года назад
9 лет назад