Question

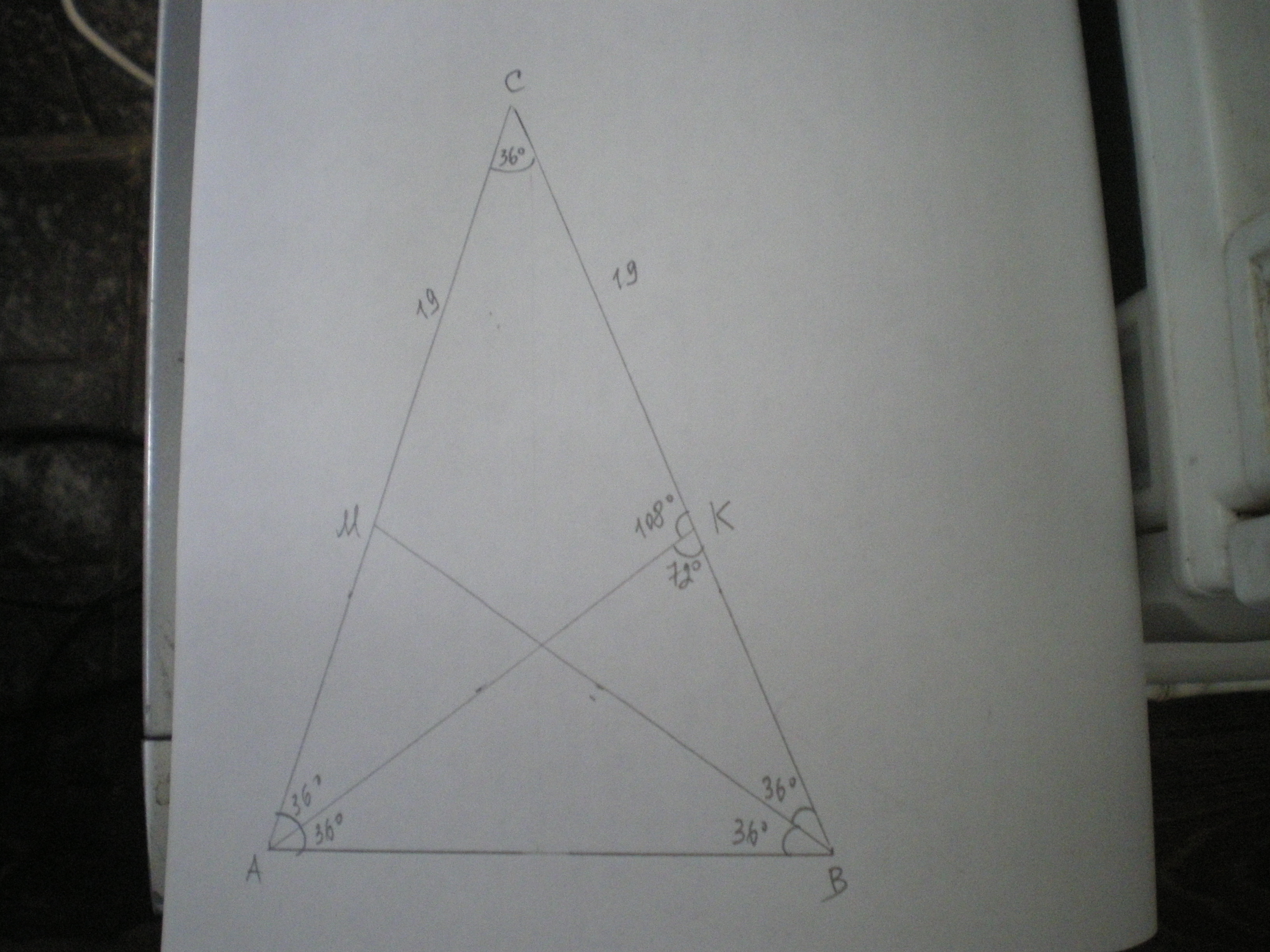
В равнобедренном треугольнике АВС угол при вершине С = 36*. ВМ и АК - биссектрисы углов В и А соответственно. Найдите длину АВ, если СМ+СК=38 см. Пожалуйста, с пояснением и чертежом.

Answer 1

СМ=СК=38:2=19 см.
∠А=∠В=(180-36):2=72°
∠САК=12 ∠А=36°
ΔАСК - равнобедренный, значит СК=АК=19 см.
∠АКС=180-(36+36)=108°
∠АКВ=180-108=72°
ΔАКВ - равнобедренный (∠В=∠АКВ=72°), значит АВ=АК=19 см.
Ответ: 19 см.