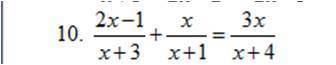Question

Решить дробно-рациональное уравнение

Answer 1

вроде так ответ решений нет

Answer 2

Спасибо большое!сейчас просмотрю.Я три раза решала и три раза по разному получилось)))

Answer 3

незачто

Answer 4

ой-ой-ой, зачем же такие большие множители

Answer 5

$displaystylemathtt{frac{2x-1}{x+3}+frac{x}{x+1}=frac{3x}{x+4};~1+frac{x-4}{x+3}+1-frac{1}{x+1}=2+frac{x-8}{x+4};~}\\\mathtt{frac{x-4}{x+3}-frac{1}{x+1}-frac{x-8}{x+4}=0;~}\\\mathtt{frac{(x-4)(x+4)(x+1)-(x+4)(x+3)-(x-8)(x+3)(x+1)}{(x+4)(x+3)(x+1)}=0}$

итак, наше уравнение эквивалентно данной системе: 

$displaystylemathtt{left{{{(x-4)(x+4)(x+1)-(x+4)(x+3)-(x-8)(x+3)(x+1)=0}}atop{xneq-4;~-3;~-1}}right}$

решим первое уравнение системы, а затем исключим из ответа ложные корни, если таковые будут

$mathtt{(x-4)(x+4)(x+1)-(x+4)(x+3)-(x-8)(x+3)(x+1)=0;~}\mathtt{x^3+x^2-16x-16-x^2-7x-12-x^3+4x^2+29x+24=0;~}\mathtt{4x^2+6x-4=(x+2)(4x-2)=0}$

следовательно, $mathtt{left[begin{array}{ccc}mathtt{x_1=-2}\mathtt{x_2=frac{1}{2}}end{array}right}$ — оба корня не противоречат области допустимых значений уравнения, поэтому являются окончательным ответом

ОТВЕТ: $mathtt{x=-2;~frac{1}{2}}$

Answer 6

Класс!спасибо!ни за что бы не догадалась..

Answer 7

пробуйте выделять целую часть в дроби, это полезно) например, имея дробь (2x – 1)/(x + 1), можно выделить целую часть: (x + 1 + x – 2)/(x + 1) = 1 + (x – 2)/(x + 1)