2. Упростите выражение:
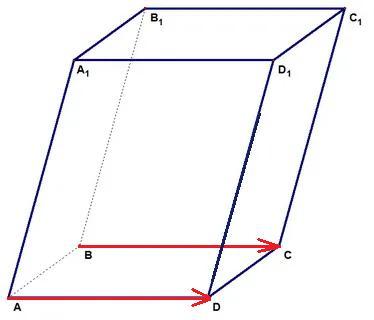
AC+BB1+BA+D1B+B1D1+DC, если ABCDA₁B₁C₁D₁ - параллелепипед.
а) AC; б)0 ; в)BB1; г)DC ; д)BA .
Ответы
Ответ дал:
0
AC + BB1 + BA + D1B + B1D1+DC=
= АС + СС₁ + С₁D₁ + D₁B +( B1D1+DC) =
= AB + (B1D1+DC) = A₁B₁ + B₁D₁ + D₁C₁ = A₁C₁
Заменяем вектор равным, чтобы применить правило "многоугольника"
= АС + СС₁ + С₁D₁ + D₁B +( B1D1+DC) =
= AB + (B1D1+DC) = A₁B₁ + B₁D₁ + D₁C₁ = A₁C₁
Заменяем вектор равным, чтобы применить правило "многоугольника"
Ответ дал:
0
В ответе надо дописать АС
Ответ дал:
0
В первой скобки применим правило треугольника, во второй скобки - правило многоугольника. Получим:
. ABCDA₁B₁C₁D₁ - параллелограмм, поэтому
Исходное выражение примет вид:
по правилу треугольника.
Ответ: а)
Приложения:
Вас заинтересует
2 года назад
3 года назад
3 года назад
9 лет назад
9 лет назад
9 лет назад