Помогите решить задачу из математического анализа. Вычислить двойной интеграл в декартовых координатах:
Приложения:
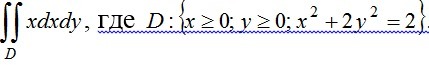
Ответы
Ответ дал:
0
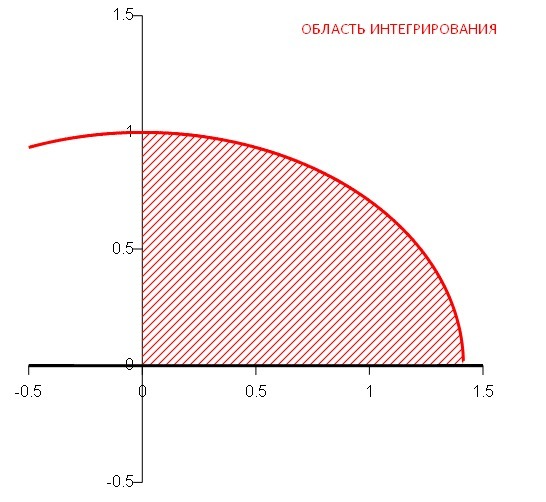
Переменная для внешнего интегрирования и ограничения для этой переменной :

Переменная для внутреннего интегрирования и ограничения для этой переменной:

![displaystyle iint_{D} xdxdy= intlimits^{sqrt{2}}_0 {} , dx intlimits^{sqrt{1- frac{x^2}{2} } }_0 {x} , dy= intlimits^{sqrt{2}}_0 {bigg[xybigg|^{sqrt{1- frac{x^2}{2} } }_0}bigg] , dx =\ \ \ = intlimits^{sqrt{2}}_0 {xsqrt{1- frac{x^2}{2} } } , dx = frac{1}{ sqrt{2} } intlimits^{sqrt{2}}_0xsqrt{2-x^2}dx= -frac{1}{2sqrt{2}} intlimits^{sqrt{2}}_0 sqrt{2-x^2} d(2-x^2)= displaystyle iint_{D} xdxdy= intlimits^{sqrt{2}}_0 {} , dx intlimits^{sqrt{1- frac{x^2}{2} } }_0 {x} , dy= intlimits^{sqrt{2}}_0 {bigg[xybigg|^{sqrt{1- frac{x^2}{2} } }_0}bigg] , dx =\ \ \ = intlimits^{sqrt{2}}_0 {xsqrt{1- frac{x^2}{2} } } , dx = frac{1}{ sqrt{2} } intlimits^{sqrt{2}}_0xsqrt{2-x^2}dx= -frac{1}{2sqrt{2}} intlimits^{sqrt{2}}_0 sqrt{2-x^2} d(2-x^2)=](https://tex.z-dn.net/?f=displaystyle++iint_%7BD%7D+xdxdy%3D+intlimits%5E%7Bsqrt%7B2%7D%7D_0+%7B%7D+%2C+dx++intlimits%5E%7Bsqrt%7B1-+frac%7Bx%5E2%7D%7B2%7D+%7D+%7D_0+%7Bx%7D+%2C+dy%3D+intlimits%5E%7Bsqrt%7B2%7D%7D_0+%7Bbigg%5Bxybigg%7C%5E%7Bsqrt%7B1-+frac%7Bx%5E2%7D%7B2%7D+%7D+%7D_0%7Dbigg%5D+%2C+dx+%3D%5C+%5C+%5C+%3D+intlimits%5E%7Bsqrt%7B2%7D%7D_0+%7Bxsqrt%7B1-+frac%7Bx%5E2%7D%7B2%7D+%7D+%7D+%2C+dx+%3D+frac%7B1%7D%7B+sqrt%7B2%7D+%7D++intlimits%5E%7Bsqrt%7B2%7D%7D_0xsqrt%7B2-x%5E2%7Ddx%3D+-frac%7B1%7D%7B2sqrt%7B2%7D%7D+intlimits%5E%7Bsqrt%7B2%7D%7D_0+sqrt%7B2-x%5E2%7D++d%282-x%5E2%29%3D)

Переменная для внутреннего интегрирования и ограничения для этой переменной:
Приложения:
Ответ дал:
0
cgfcb,j ,jkmijt
Ответ дал:
0
спасибо большое
Вас заинтересует
2 года назад
2 года назад
3 года назад
3 года назад
9 лет назад
9 лет назад
10 лет назад