Question

Help!!!!!!!!!!!!!!!!! пожалуйста, очень срочно. помогите

Answer 1

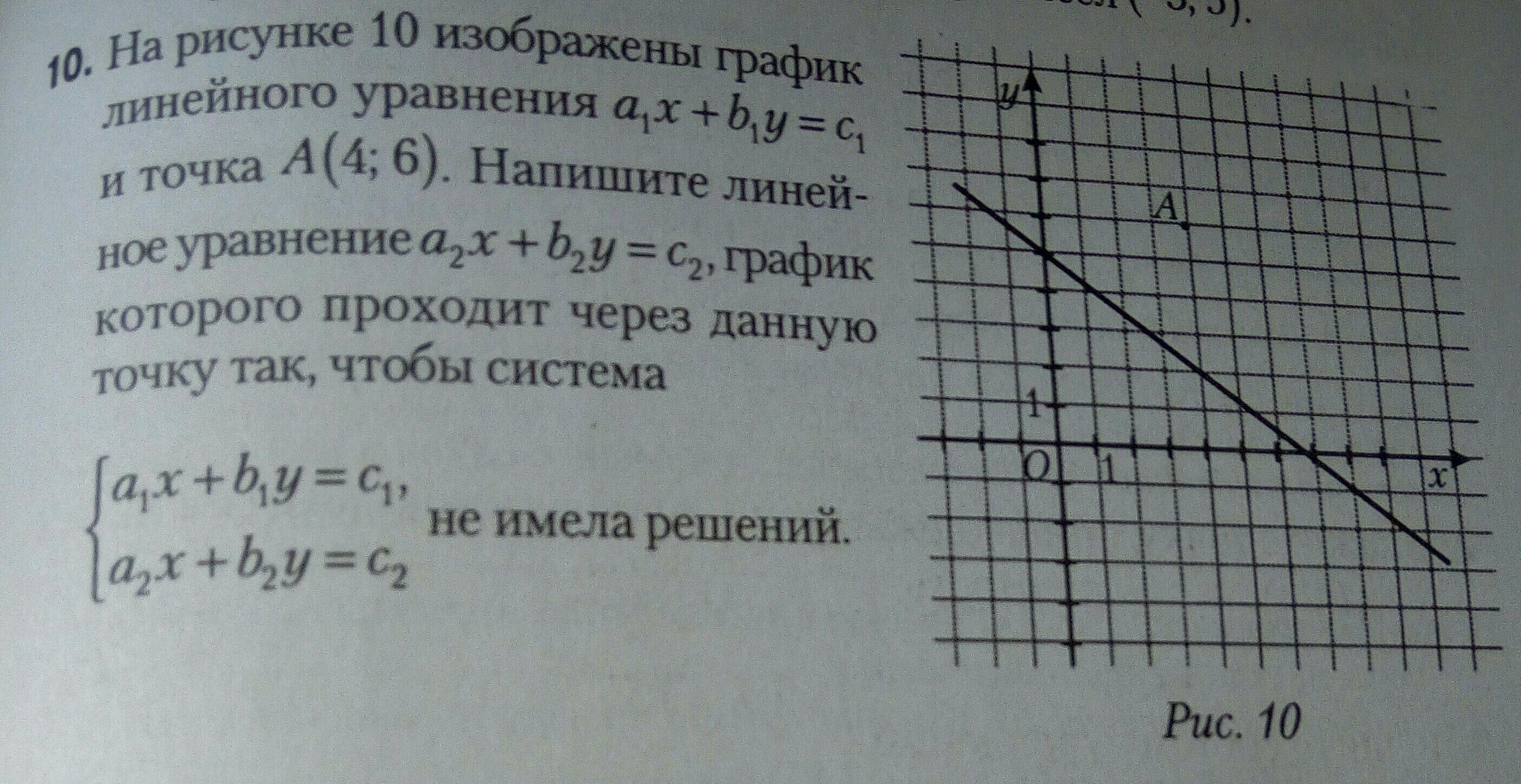
Чтобы система не имела решений, прямые должны быть параллельны.
т.е. если:  $a_{1} x+ b_{1} y = c_{1}$, то
$y = frac{-a_{1} }{b_{1} } x+ frac{ c_{1} }{b_{1} }$
и
$y = frac{-a_{2} }{b_{2} } x+ frac{ c_{2} }{b_{2} }$

при параллельности: $frac{a_{2} }{b_{2} } = frac{a_{1} }{b_{1} }$


Первая прямая проходит через точки (0;5) и (4;2) подставим эти точки в уравнение $y = frac{-a_{1} }{b_{1} } x+ frac{ c_{1} }{b_{1} }$:
$5 = frac{-a_{1} }{b_{1} } *0+ frac{ c_{1} }{b_{1} }$
$frac{ c_{1} }{b_{1} } = 5$
и 
$2 = frac{-a_{1} }{b_{1} } *4+ frac{ c_{1} }{b_{1} }$
$2 = frac{-a_{1} }{b_{1} } *4+ 5$
$5-2 = frac{a_{1} }{b_{1} } *4$
$frac{a_{1} }{b_{1} } =frac{3}{4}$

Значит: $frac{a_{2} }{b_{2} } = frac{a_{1} }{b_{1} } =frac{3}{4}$
Тогда вторая прямая примет вид: $y = -frac{3}{4} x+ frac{ c_{2} }{b_{2} }$
По графику видно, что он проходит через точку А(4;6), подставим:
$6 =- frac{3}{4} *4+ frac{ c_{2} }{b_{2} }$
$6 = -3+ frac{ c_{2} }{b_{2} }$
$frac{ c_{2} }{b_{2} } = 9$

Теперь соберем это вместе: $y = -frac{3}{4} x+9|*4$
Преобразуем в стандартный вид:
$4y = -3x+36$
$4y +3x = 36$

Ответ: $4y +3x =36$

Answer 2

как такое можно решить на ср или кр

Answer 3

ответ 4y +3x =36 точно верный. решила другим методом по построению - такой же ответ, так что скорее всего в самих ответах опечатка

Answer 4

ок, спасибо за старарния

Answer 5

огромное спасибо

Answer 6

))