Question

прямая параллельная стороне АС треугольника АВС,пересекает сторону АВ в точке А1 ,а Сторону ВС в точке С1, Докажите что углы треугольника АВС равны углам треугольника А1ВС1

Answer 1

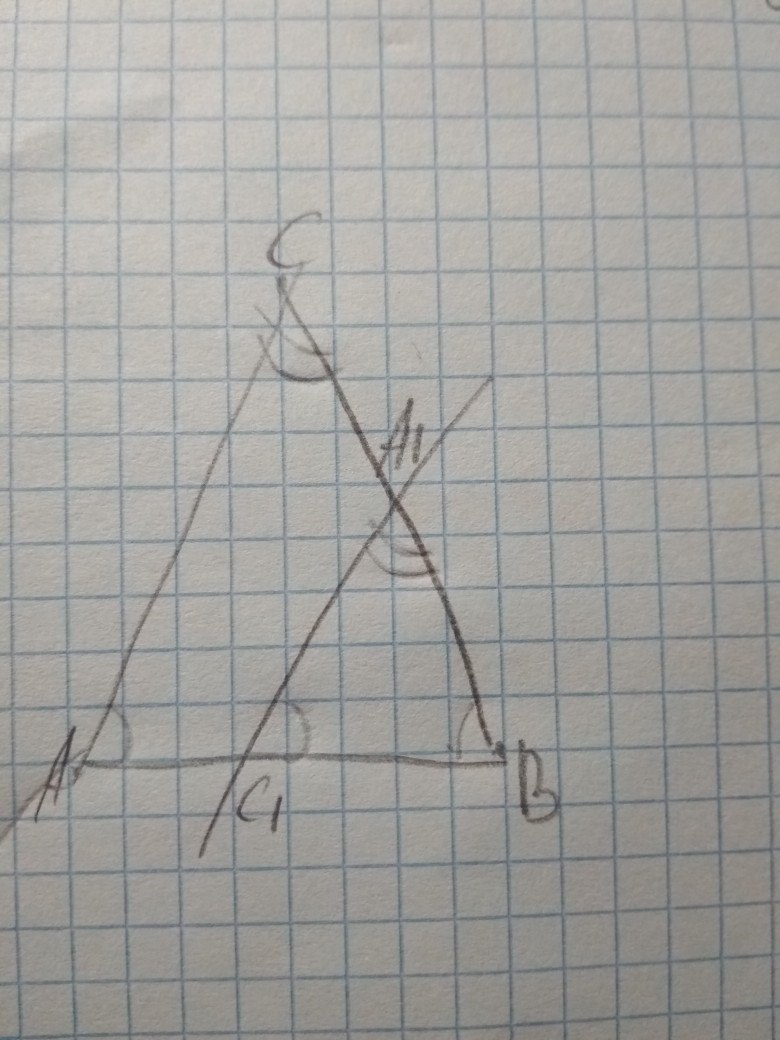
У нас получились 2 треугольника,(можешь продлить сторону AC). АВ секущая параллельных прямых AC и A1C1 следует, что угол A равен углу C1(односторонние помоему). Далее, CB секущая двух параллельных AC и A1C1 следует угол C равен углу A1, а поскольку B общий угол, значит углы треугольника ACB равны углам треугольника A1C1B
 Ч.т.д.

Answer 2

Ответ:

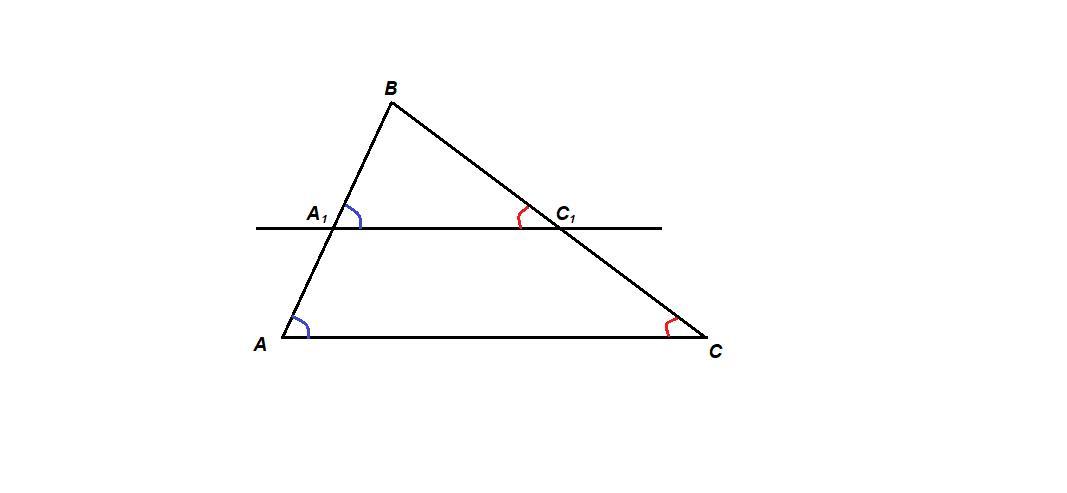
∠ВАС = ∠ВА₁С₁ как соответственные при пересечении параллельных прямых АС и А₁С₁ секущей АВ,

∠ВСА = ∠ВС₁А₁ как соответственные при пересечении параллельных прямых АС и А₁С₁ секущей ВС.

Угол при вершине В общий для треугольников АВС и А₁ВС₁.

Значит, углы треугольника АВС равны соответствующим углам треугольника А₁ВС₁.