Ответы
Ответ дал:
0
Если что-то непонятно - пишите
Приложения:
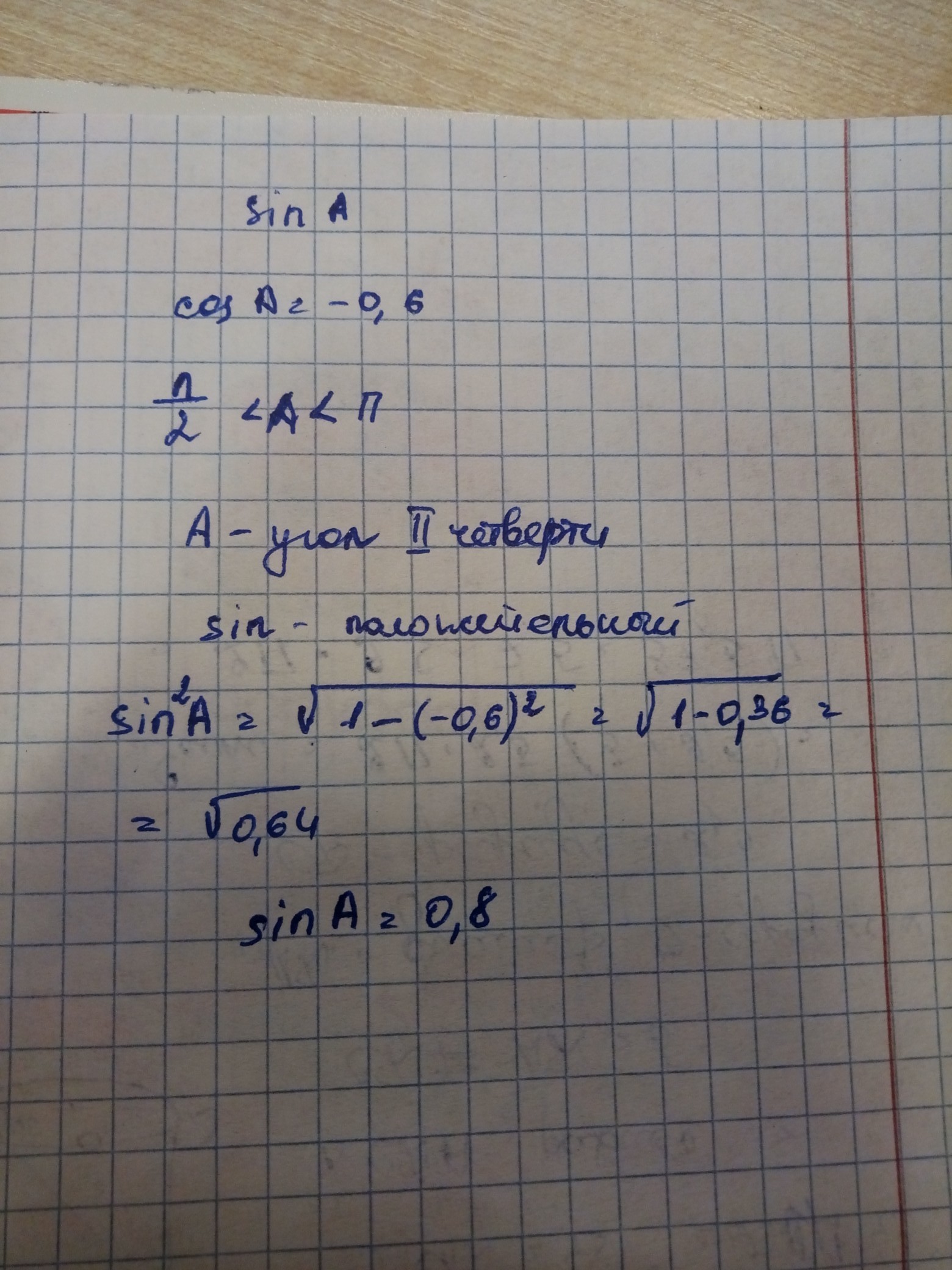
Ответ дал:
0
Ответ:
sin a = 0,8
Пошаговое объяснение:
Воспользуемся формулой
sin²a=1-cos²a
Известно: cosa = -0,6 и
Угол a принадлежит ко второму квадранту и поэтому sin a≥0. Тогда
Ответ дал:
0
Ответ:
0,8.
Пошаговое объяснение:
Воспользуемся основным тригонометрическим тождеством:
Так как угол второй четверти , синус в этой четверти положительный , то
Вас заинтересует
2 года назад
2 года назад
3 года назад
3 года назад
9 лет назад
9 лет назад
10 лет назад