Одна из сторон треугольника равна 13 см, а другая сторона точкой касания вписанной окружности делится на отрезки 6 см и 8 см, считая от известной стороны. Найдите радиус окружности, вписанной в этот треугольник.
Ответы
Ответ дал:
0
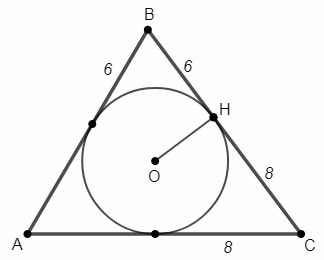
AB=13
H - точка касания вписанной окружности на стороне BC
BH=6, CH=8
По теореме об отрезках касательных, проведенных из одной точки
AC=AB-BH+CH =13-6+8 =15
По формуле Герона
p= (a+b+c)/2 =(13+14+15)/2 =21 (полупериметр)
r= √( (p-a)(p-b)(p-c)/p ) =√( 8*7*6/21 ) =4 (см)
H - точка касания вписанной окружности на стороне BC
BH=6, CH=8
По теореме об отрезках касательных, проведенных из одной точки
AC=AB-BH+CH =13-6+8 =15
По формуле Герона
p= (a+b+c)/2 =(13+14+15)/2 =21 (полупериметр)
r= √( (p-a)(p-b)(p-c)/p ) =√( 8*7*6/21 ) =4 (см)
Приложения:
Вас заинтересует
2 года назад
2 года назад
3 года назад
3 года назад
9 лет назад
10 лет назад