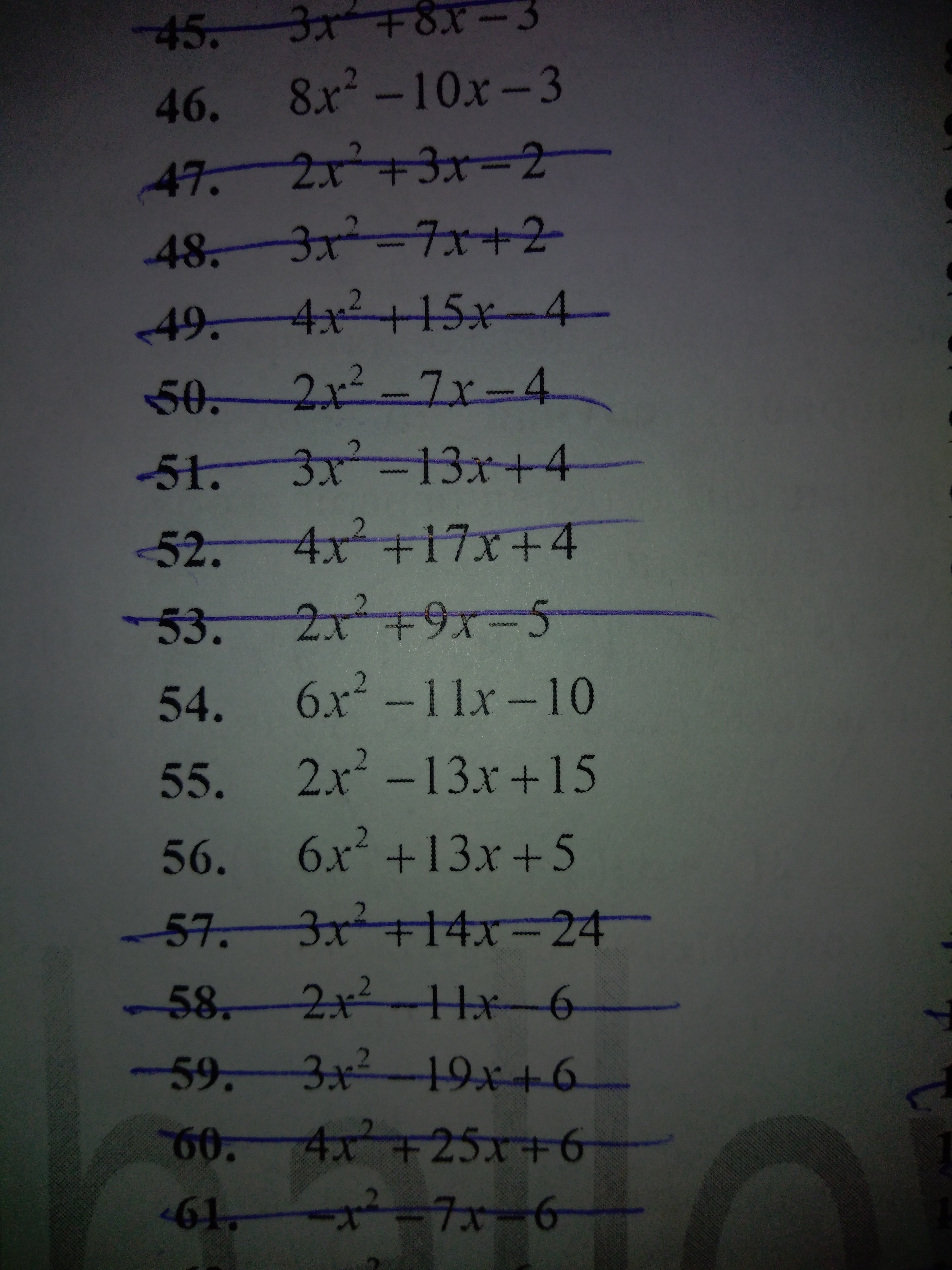Question

Объясните как разложить на множители 54 пример через дискриминант. Не могу понять.

Answer 1

Теоретическая часть: многочлен вида ax²+bx+c можно разложить на множители в виде: a(x-x1)(x-x2), где х1 и х2 - корни квадратного уравнения аx²+bx+c=0.
В нашем примере:
6x²-11x-10=6(x-x1)(x-x2), где х1 и х2 - корни уравнения 6х²-11х-10=0.
Найдём корни этого уравнения через дискриминант: D=b²-4ac, D=(-11)²-4*6*(-10)=121+240=361=19²
x1=(-b-√D)/2a=(11-19)/(2*6)=-8/12=-2/3,
x2=(-b+√D)/2a=(11+19)/(2*6)=30/12=2,5.
Тогда 6x²-11x-10=6(х+2/3)(х-2,5)

Answer 2

Я тоже так решал, но в ответнике другой ответ

Answer 3

в ответниках не всегда верные ответы. проверка подтверждает верность решения.

Answer 4

В ответнике, наверное, число 6 разложили на множители (3*2), а затем первый множитель внесли в первую скобку, а второй - во вторую: (3х+2)(2х-5)